跳到主要内容

动手学深度学习笔记

动手学深度学习 d2l-ai/d2l-zh: 《动手学深度学习》：github 仓库

第十章 注意力机制​

注意力提示​

生物学中的注意力​

1. 非自主性提示（被动注意）​
  • 靠“突出性”吸引注意力：不需要主动思考，环境中明显的事物会自动抓住眼球。
    • 例子：一堆黑白物品中放一个红色咖啡杯，你会不自觉先看向它
2. 自主性提示（主动注意）​
  • 靠“主观目标”引导注意力=：需要意识控制，根据任务主动选择关注对象。
    • 例子：喝完咖啡后，你想读书，就会主动转头看向书。

神经网络中的注意力机制：查询、键与值​

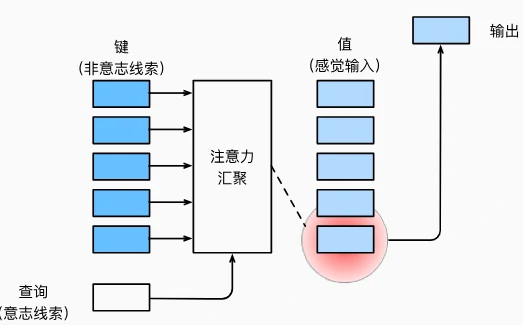注意力机制查询键值示意图 - **核心思想**：模仿人类的注意力选择，让机器学会“有重点”地处理信息。 - 三个关键概念： - **查询（Query）**：相当于**自主性提示，是机器的“目标”**（比如想翻译某个词）。 - **键（Key）**：相当于**非自主性提示，是信息的“特征标签”**（比如句子中每个词）。 - **值（Value）**：是**实际需要处理的信息**（比如词的具体语义）。 - 工作原理： - 机器根据“查询”（目标），在一堆“键”中寻找匹配的信息，然后从对应的“值”中提取有用内容。 - 比如翻译 “苹果”，它心里的目标（Query）是 “找这个词在英文里咋说”，然后看上下文里的各种 “标签”（Key：吃的、手机），最后从对应的 “内容”（Value）里挑出最合适的 —— 吃的就选 “apple”，手机就选 “iPhone”。

19-三种注意力机制对比

注意力的可视化：用热力图看重点​

  • 如何可视化注意力？：通过绘制“热力图”展示查询和键之间的权重（关注度）。用 Python 的show_heatmaps函数，会经常用到。 如果查询和键完全匹配，权重为 1（颜色最深）；不匹配则权重为 0（颜色最浅）。

注意力汇聚​

问题背景：如何预测数据​

假设我们有一堆带噪声的训练数据（比如 50 个点），想根据这些数据学习一个函数，预测新输入值对应的输出。 举个例子：输入是“时间”，输出是“气温”，用历史数据预测未来气温。

简单基线：平均汇聚（笨方法）​

最偷懒的方法是直接取所有训练数据输出的平均值，不管输入是什么。 缺点：预测结果是一条水平直线，完全忽略输入之间的差异，和真实结果差距很大

升级方案：非参数注意力汇聚（Nadaraya-Watson 核回归）​

核心思想​
  • 预测新输入 x 时，不是平均看所有数据，而是重点关注和 x 相似的训练数据。
  • 用“距离”衡量相似性：离 x 越近的训练点，权重越高（获得更多注意力）；离得越远，权重越低。
数学原理​
  • 权重公式：$$\text{权重} = \frac{\exp(-\frac{(x - x_i)^2}{2})}{\sum_j \exp(-\frac{(x - x_j)^2}{2})}$$ 简单说：距离越近，指数值越大，权重越高（类似“物以类聚”）。
  • 预测结果：所有训练输出的加权平均，权重由上述公式计算。
效果：​
  • 预测线变得平滑，且更接近真实函数。
  • 可视化注意力权重：热力图中颜色越深，表示对应训练点的权重越高（查询和键越接近，权重越高）。

进阶：带参数的注意力汇聚（可学习版本）​

非参数模型虽然有效，但缺乏可学习的参数。于是引入一个参数w，用来调整距离的“敏感度”：

  • 公式变成：$$\text{权重} = \frac{\exp(-\frac{(x - x_i)^2 w^2}{2})}{\sum_j \exp(-\frac{(x - x_j)^2 w^2}{2})}$$
    • w 越大：距离的影响被放大，模型更“挑剔”，只关注非常近的点；
    • w 越小：距离的影响被缩小，模型更“包容”，关注范围更广。

训练方法​

  • 通过深度学习框架（如 PyTorch、TensorFlow）训练参数 w，让预测结果和真实值的差距最小。
  • 利用批量矩阵乘法加速计算，提高效率。

注意力评分函数​

注意力机制中的评分函数，它决定了如何计算查询和键之间的匹配度，从而生成注意力权重。加性和缩放点积注意力分别适用于不同长度和等长向量，后者在效率和性能上更优，广泛应用于现代 NLP 模型（如 BERT、GPT）。掩蔽 softmax 用于过滤无效数据，确保注意力仅集中在有效信息上；。

注意力评分函数​

注意力机制的核心是根据查询（目标）和键（特征标签）的匹配度，给不同的值（信息）分配权重。 评分函数就是用来计算这种匹配度的公式，输出的分数经过 softmax 后变成概率分布（注意力权重），最终加权求和得到输出。

20-注意力评分函数计算流程

图中 a(q, k)就是评分函数，输出分数后通过 softmax 得到权重 α，再乘以值 v 得到结果。

掩蔽 softmax：过滤无效数据​

在处理文本等序列数据时，经常会遇到填充的无效词元（如用“”填充短句子）。掩蔽 softmax的作用是：

  • 将无效位置的分数设为负无穷（如-1e6），经过 softmax 后这些位置的权重接近 0，从而被忽略。
  • 例子：假设有两个样本，有效长度分别为 2 和 3，掩蔽后超出长度的位置权重为 0。
输入分数矩阵：
[[0.5, 0.3, 0.2, 0.1],   # 有效长度2，第3、4位无效
 [0.4, 0.3, 0.2, 0.1]]   # 有效长度3，第4位无效
掩蔽后：
[[0.5, 0.3, -inf, -inf],
 [0.4, 0.3, 0.2, -inf]]
softmax结果：
[[0.62, 0.38, 0,   0],
 [0.46, 0.35, 0.19, 0]]

加性注意力：处理不同长度的查询和键​

当查询和键的长度不同时（比如查询是 20 维，键是 2 维），可以用加性注意力：

  • 原理：将查询和键分别输入两个神经网络（Wq 和 Wk），再将结果相加，通过 tanh 激活后，用第三个网络（wv）输出分数。 $$a(q, k) = w_v^\top \tanh(W_q q + W_k k)$$
  • 特点：通过神经网络学习匹配度，适合处理不同长度的向量，但计算量较大。
  • 代码实现：用 PyTorch 等框架定义三个线性层，计算时扩展维度后相加，再输出分数。

缩放点积注意力：高效处理等长向量​

当查询和键长度相同时（均为 d 维），缩放点积注意力更高效：

  • 原理：直接计算查询和键的点积，除以 √d（防止数值过大），再通过 softmax 得到权重。$$a(q, k) = \frac{q \cdot k}{\sqrt{d}}$$ 将原本的上下文向量变为每个词都带对应当前词的权重的向量
  • 特点：计算量仅为矩阵乘法，效率高，适合大规模数据（如 Transformer 模型）。
  • 代码实现：用batch_dot计算点积，除以根号 d，再用掩蔽 softmax 处理无效位置。

Bahdanau 注意力​

Bahdanau 注意力机制核心是让解码器在生成每个词时，能动态选择输入序列中的相关部分，而不是固定使用整个输入的上下文。

传统编码器-解码器的不足​

在传统的机器翻译模型（如循环神经网络编码器-解码器）中，编码器会把整个输入序列压缩成一个固定长度的“上下文变量”，解码器生成每个词时都使用这个固定变量。问题：输入序列中并非所有词都对当前生成的词有用。例如翻译“我吃饭”时，“我”和“饭”对生成“eat”的重要性不同，但传统模型无法区分。

Bahdanau注意力：动态选择相关信息​

Bahdanau 注意力的核心思想是：解码器在生成每个词时，动态计算输入序列中每个词的权重，只关注与当前生成任务相关的部分。

  • 关键概念：
    • 查询（Query）：解码器上一时间步的隐状态（代表当前生成的“目标”）。
    • 键（Key）和值（Value）：编码器每个时间步的隐状态（键值对相同，代表输入序列的不同位置）。
    • 注意力权重：通过加性注意力评分函数计算查询与每个键的匹配度，再用 softmax 转化为权重，决定对应值的重要性。
  • 公式：$$c_{t'} = \sum_t \alpha(s_{t'-1}, h_t) h_t$$ 其中，$c_{t'}$是当前上下文变量，$\alpha$是注意力权重，$s_{t'-1}$是解码器上一步隐状态，$h_t$是编码器第 t 步隐状态。

模型结构：带注意力的解码器​

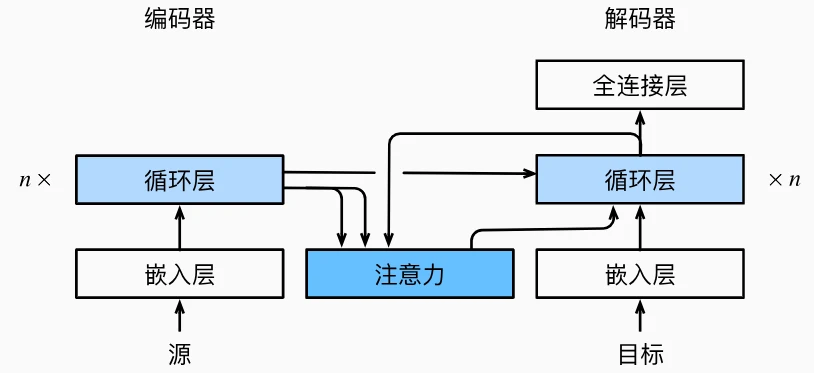
21-Bahdanau注意力解码器结构

编码器：与传统模型相同，将输入序列编码为各时间步的隐状态$h_t$（形状为$(\text{批量大小}, \text{时间步}, \text{隐藏层维度})$） 解码器：每步生成词时，执行以下操作：

  1. 查询生成：用上一时间步的解码器隐状态$s_{t'-1}$作为查询。
  2. 注意力计算：用加性注意力计算查询与所有编码器隐状态的权重，得到上下文变量$c_{t'}$。
  3. 输入拼接：将上下文变量$c_{t'}$与当前输入词的嵌入向量拼接，作为循环神经网络（如 GRU）的输入。
  4. 生成词元：通过全连接层预测当前词的概率。 特点：解码器每步的上下文变量$c_{t'}$都是动态计算的，依赖于当前生成目标。

训练与效果：动态对齐输入输出​

  • 训练流程：
    1. 编码器处理输入序列，得到各时间步隐状态。
    2. 解码器逐步生成输出序列，每步使用注意力选择输入中的相关部分。
    3. 通过反向传播训练整个模型（编码器+解码器+注意力参数）。
  • 可视化注意力权重： 训练后观察发现，解码器生成每个词时，注意力权重会集中在输入序列的相关位置。例如翻译“i'm home”时，“home”对应的权重集中在输入的“home”词元上。
  • 性能：相比传统模型，Bahdanau 注意力提升了翻译准确性（如 BLEU 分数更高），但由于每步都要计算注意力，训练速度较慢。

第十一章 优化算法​

优化和深度学习​

优化 vs 深度学习：目标不同​

对于深度学习问题，我们通常会先定义损失函数。一旦我们有了损失函数，我们就可以使用优化算法来尝试最小化损失。在优化中，损失函数通常被称为优化问题的目标函数。

  • 优化的目标：最小化目标函数（如训练损失），关注如何快速找到损失函数的最低点。
  • 深度学习的目标：降低模型的泛化误差（在新数据上的误差），不仅需要优化训练损失，还要防止过拟合（如通过正则化、数据增强等）。
  • 关键区别：优化只盯着训练数据，而深度学习要兼顾训练和泛化。例如，训练损失最低的模型不一定在真实数据上表现最好。

优化的三大挑战​

局部最小值Local Minima​
  • 定义：函数的某个点比周围点都低，但不是全局最低（像山谷中的小坑）。
  • 问题：优化算法可能被困在局部最小值，无法找到全局最优解。
  • 应对：使用随机梯度下降（SGD）等带随机性的算法，利用噪声跳出局部最小值。
2. 鞍点Saddle Points​
  • 定义：梯度为零，但既不是最小值也不是最大值的点（像马鞍中间的点，前后高左右低）。
  • 问题：优化算法在鞍点处梯度消失，导致停滞。
  • 例子：
    • 一维函数$f(x) = x^3$在$x=0$处是鞍点（导数为 0，但左右两边函数值一升一降）。
    • 二维函数$f(x,y) = x^2 - y^2$在原点 (0,0) 处是鞍点。
  • 数学原理：高维函数的鞍点更常见，因为 Hessian 矩阵（二阶导数矩阵）可能同时有正负特征值。
3. 梯度消失Vanishing Gradient​
  • 定义：梯度变得极小，导致参数更新缓慢甚至停滞。
  • 原因：深层网络中激活函数（如 sigmoid、tanh）的导数趋近于零，反向传播时梯度逐层衰减。
  • 例子：函数$f(x) = \tanh(x)$在$x=4$附近梯度接近 0（$f'(4) \approx 0.0013$），优化难以推进（见下图）。
  • 应对：使用 ReLU 等激活函数、残差连接、批量归一化等技术缓解梯度消失。

凸性​

凸集与凸函数​

凸集Convex Set​

  • 直观理解：如果集合中任意两点连成的线段都完全包含在集合内，这个集合就是凸集。
    • 圆形、正方形是凸集（任意两点连线在内部）。
    • 空心圆环是非凸集（两点连线可能穿过空心部分，不在集合内）。
  • 数学定义：对集合内任意两点$a, b$和任意$λ∈[0,1]$，有$λa + (1-λ)b$也在集合内。
  • 性质： 凸集的交集仍是凸集，但并集不一定是凸集。

2. 凸函数Convex Function​

  • 直观理解：函数图像呈“向上凸”（如抛物线$f(x)=0.5x²$），任意两点间的线段始终在函数图像上方。
    • 非凸函数例子：余弦函数$f(x)=\cos(πx)$有多个波峰波谷，不满足凸性（如图中中间子图）。
  • 数学定义：对凸集内任意两点$x, x'$和$λ∈[0,1]$，有$λf(x) + (1-λ)f(x') ≥ f(λx + (1-λ)x')$。
  • 詹森不等式（Jensen’s Inequality）：凸函数的期望不小于期望的凸函数，即$E[f(X)] ≥ f(E[X])$。例如，用简单分布估计复杂分布的下界。

凸函数的关键性质​

局部最小值 = 全局最小值​
  • 核心结论：凸函数中，任何局部最小值都是全局最小值。
    • 证明思路：假设存在一个局部最小值不是全局最小，会推导出矛盾（利用凸性定义）。
    • 例子：$f(x)=(x-1)²$的局部最小值$x=1$也是全局最小值（如图）。
  • 意义：凸优化问题不存在“被困在局部最优”的问题，优化算法更容易找到全局解。
2. 下水平集是凸集​
  • 下水平集：所有满足$f(x)≤b$的点构成的集合$S_b$。
  • 性质：凸函数的下水平集一定是凸集。
    • 应用：帮助分析优化问题的可行解区域是否凸，简化约束条件。
3. 二阶导数与凸性​
  • 一维情况：函数二阶导数$f''(x)≥0$时是凸函数（如抛物线的二阶导数为常数 2>0）。
  • 高维情况：Hessian 矩阵（二阶导数矩阵）半正定（所有特征值 ≥0）时，函数是凸函数。
    • 例子：$f(x,y)=x²+y²$的 Hessian 矩阵是单位矩阵，半正定，因此是凸函数。

梯度下降​

**梯度下降（Gradient Descent）算法的基本原理，从一维情况延伸到多维场景，学习率对优化效果的影响，以及在非凸函数中的挑战。

梯度下降的核心思想：沿着最陡下坡走​

  • 目标：找到函数的最小值（如损失函数的最低点）。
  • 原理：
    1. 利用泰勒展开近似，函数在某点的局部下降最快方向是负梯度方向。
    2. 每次迭代沿着负梯度方向更新参数，逐步接近最小值。

一维梯度下降​

  1. 核心原理
    • 利用泰勒展开近似函数：f(x+ϵ) ≈ f(x) + ϵf'(x)，取ϵ = -ηf'(x)（η为学习率），得更新公式x ← x - ηf'(x)，确保函数值下降（f(x-ηf'(x)) ≤ f(x)，当f'(x)≠0且η足够小）。
    • 示例：目标函数f(x)=x²，导数f'(x)=2x，初始值x=10，η=0.2时，10 次迭代后x≈0.0605，接近最小值x=0。
  2. 学习率的关键作用 学习率η决定参数更新步长。过小会导致x更新缓慢，需更多迭代才能收敛（如η=0.05时 10 步后仍远离最优解）；过大则可能使x跳过最小值甚至发散（如η=1.1时x逐渐增大），因泰勒展开的高阶项误差显著，无法保证函数值下降。
  3. 局部最小值陷阱
    • 非凸函数（如f(x)=x·cos(0.15πx)）存在多个局部最小值，高学习率（如η=2）可能导致收敛到较差的局部解（如x≈-1.528）。

多元梯度下降​

  1. 梯度向量与更新规则
    • 目标函数f: R^d→R，梯度∇f(x)为各变量偏导数组成的向量，更新公式为x ← x - η∇f(x)。
    • 示例：二维函数f(x1,x2)=x1²+2x2²，梯度(2x1,4x2)，初始值(-5,-2)，η=0.1时，20 次迭代后x1≈-0.0576，x2≈-0.000073，接近最小值(0,0)，但收敛速度较慢。
  2. 变量尺度问题
    • 不同变量梯度幅值差异大（如x1梯度为2x1，x2梯度为4x2），导致更新方向偏离最优路径，需通过预处理调整各变量学习率。

自适应优化方法​

  1. 牛顿法（二阶方法）
    • 原理：利用泰勒展开二阶项，引入 Hessian 矩阵H=∇²f(x)，更新公式为x ← x - H⁻¹∇f(x)。
    • 优势：凸函数中收敛迅速（如f(x)=0.5x²一步到位），接近极小值时误差呈二次收敛（|e(k+1)| ≤ c|e(k)|²）。
    • 劣势：非凸函数中 Hessian 可能为负，导致函数值上升（如f(x)=x·cos(0.15πx)迭代后x=26.834）；计算 Hessian 矩阵复杂度高（O(d²)），不适合高维场景。
  2. 预处理（简化牛顿法）
    • 仅计算 Hessian 对角线元素diag(H)，更新公式为x ← x - ηdiag(H)⁻¹∇f(x)，解决变量尺度不匹配（如毫米与公里单位的参数），提升收敛效率。
  3. 线搜索
    • 沿梯度方向搜索最优学习率（如二分法），确保f(x-η∇f(x))最小化，理论收敛快，但每步需评估全数据集，不适合深度学习。

随机梯度下降​

随机梯度下降（SGD）核心机制​

简而言之就是随机采样来减少计算量。

  • 目标函数：数据集上的平均损失函数，即$f(x) = \frac{1}{n}\sum_{i=1}^n f_i(x)$。
  • 梯度下降（GD）：计算完整梯度$\nabla f(x) = \frac{1}{n}\sum_{i=1}^n \nabla f_i(x)$，计算复杂度 O(n)。
  • SGD 核心创新：随机选取单个样本$i$，用其梯度$\nabla f_i(x)$更新参数，即$x \leftarrow x - \eta \nabla f_i(x)$，计算复杂度骤降至 O(1)。
  • 无偏估计性质：随机梯度是完整梯度的无偏估计，即$\mathbb{E}_i[\nabla f_i(x)] = \nabla f(x)$。

动态学习率策略​

  1. 必要性

    • SGD 梯度含噪声，固定学习率易导致：
      • 学习率过大：参数剧烈振荡（如 η=0.1 时，50 次迭代后 x2 波动范围达 0.11~0.23）；
      • 学习率过小：收敛缓慢（如指数衰减 η=0.1e^(-0.1t)，1000 次迭代后 x1 仍偏离 0.82）。

  2. 三种核心策略

策略数学公式特点与效果
分段常数$\eta(t) = \eta_i$（分段常数）手动调整（如训练停滞时降低），深度学习常用，灵活性高但依赖经验。
指数衰减$\eta(t) = \eta_0 \cdot e^{-\lambda t}$衰减速度快，易过早陷入次优解（如 1000 次迭代后 x1=-0.77，离最优解 0.77）。
多项式衰减$\eta(t) = \eta_0 \cdot (βt + 1)^{-\alpha}$（α=0.5 时）凸优化中表现优异，50 次迭代后 x2 接近 0（如示例中 x2=-0.0006），平衡衰减速度与精度。

凸目标函数的收敛性分析​

  1. 理论假设
    • 目标函数$f(\xi, x)$凸，梯度 L2 范数有界：$|\nabla f(\xi, x)| \leq L$。
    • 初始参数与最优解距离：$|x_1 - x^*| = r$。
  2. 关键结论
    • 收敛速度：按 O(1/T) 收敛至最优解，即迭代 T 次后，期望风险与最优风险差$E[R(\bar{x})] - R^* \leq \frac{r^2 + L^2\sum\eta_t^2}{2\sum\eta_t}$。
    • 最优学习率：$\eta = \frac{r}{LT}$，平衡初始距离与梯度噪声。

有限样本与实际应用​

采样策略对比

  • 有放回采样：单个样本被选中概率约 63%，数据重复导致方差大，效率低。
  • 无放回采样：遍历所有样本（本书默认），减少方差，提升数据利用效率。

关键问题​

  1. SGD 为什么能在大规模数据中高效优化？ SGD 每次迭代仅计算单个样本的梯度，将计算复杂度从梯度下降的 O(n) 降至 O(1)，避免了全量数据计算的时间和内存开销。尽管引入随机噪声，但随机梯度是完整梯度的无偏估计，平均意义上仍能逼近最优解，尤其适合 n 极大的深度学习场景（如百万级样本）。
  2. 凸函数与非凸函数下 SGD 的收敛性有何差异？
  • 凸函数：有严格理论保证，收敛速度为 O(1/T)，通过设置学习率$\eta = r/(LT)$可确保按次线性速率逼近最优解；
  • 非凸函数：缺乏强收敛保证，可能陷入局部最小值（数量可能指数级），但实践中 SGD 的噪声特性可能帮助跳出浅局部最小值，需依赖经验调参（如动态学习率、初始化策略）提升效果。

小批量随机梯度下降​

核心动机：平衡效率与稳定性​

  1. 两种极端方法的缺陷
    • 梯度下降（GD）：每次迭代计算全量数据梯度（O(n)），计算成本随数据量 n 线性增长，数据相似时“数据低效”。
    • 随机梯度下降（SGD）：每次仅用单个样本（O(1)），梯度噪声大（轨迹嘈杂），且 CPU/GPU 无法充分利用向量化（频繁单样本操作导致框架开销大）。
    • 小批量 SGD：取中间路径，每次处理 b 个样本（O(b)），b 通常为 16-1024，平衡计算效率与梯度稳定性。
  2. 核心目标
    • 计算高效：利用硬件向量化和缓存优化，减少内存访问开销。
    • 梯度稳定：通过平均 b 个样本梯度，降低随机噪声（方差随 b 增大而减小）。

向量化与缓存优化：提升计算效率的关键​

  • CPU/GPU 架构：寄存器（最快，容量最小）→ L1/L2 缓存（中等）→ L3 缓存（共享）→ 主内存（最慢，容量最大）。
  • 带宽差距：CPU 计算能力可达 10^12 字节/秒，而内存带宽通常仅 100 Gb/s（约为计算能力的 1/10），导致“内存墙”问题。
  • 结论：向量化操作（如一次性矩阵乘法）可显著提升计算效率，小批量处理利用这一特性减少内存访问次数。

小批量的核心优势：梯度与方差平衡​

  1. 梯度统计特性
    • 无偏性：小批量梯度是全量梯度的无偏估计，即$\mathbb{E}[g_{batch}] = \nabla f(x)$。
    • 方差降低：假设单个样本梯度标准差为 σ，小批量梯度标准差为$\sigma / \sqrt{b}$（b 为批量大小），例如 b=64 时，标准差降至 1/8。
  2. 实际效果与批量大小选择
    • 计算效率：批量大小 64 时，块矩阵乘法性能达 312.681 Gigaflops，接近全矩阵计算的 56%（555.868 Gigaflops）。
    • 内存限制：批量大小受限于 GPU 显存（如 1024 样本可能占用数 GB 显存），需在效率与内存之间权衡。
    • 正则化效应：较小批量（如 32）引入更多噪声，可能具有正则化效果（类似 SGD）；较大批量（如 1024）梯度更稳定，但可能陷入局部最小值。

实现与实验：从数据到代码​

  1. 数据预处理（NASA 机翼噪声数据集）

    • 样本数：1500，特征维度：5，标签：噪声级别。
    • 处理步骤：去均值、缩方差（标准化），确保各特征同分布。

  2. 优化器与训练函数实现

    • 优化器（sgd 函数）：

      def sgd(params, states, hyperparams):
          for p in params:
              p[:] -= hyperparams['lr'] * p.grad  # 批量梯度更新

    • 训练函数 train_ch11：

      • 初始化线性回归模型（权重 w、偏置 b）。
      • 迭代小批量数据，计算平均损失并反向传播，更新参数。
      • 监控训练过程，每 200 样本打印损失（目标范围：0.22-0.35）。

  3. 批量大小的实践建议

    • CPU 场景：批量大小 32-128（受限于缓存容量）。
    • GPU 场景：批量大小 128-1024（利用显存和并行计算能力）。
    • 极端案例：超大批量（如 8192）可能导致梯度不稳定，需配合学习率调整（如线性缩放学习率）。

关键问题​

为什么小批量 SGD 比单样本 SGD 计算效率更高？

  • 答案：单样本 SGD 每次执行单个矩阵-向量乘法，频繁访问内存且无法利用 CPU/GPU 的向量化指令（如 AVX-512），导致框架开销大（每次调用触发调度）。小批量 SGD 通过一次性处理 b 个样本，将操作合并为矩阵运算（如批量矩阵乘法），充分利用硬件缓存和向量化，减少内存访问次数（如全矩阵计算性能比按元素计算高 3.4 万倍），同时降低框架交互开销。

小批量大小如何影响梯度的稳定性和计算效率？

  • 答案：
    • 梯度稳定性：批量大小 b 越大，梯度方差越小（标准差降为 1/√b），更新方向越接近全量梯度（如 b=64 时方差减少 87.5%）。
    • 计算效率：b 增大提升向量化效率（如 b=64 时块矩阵乘法达 312 Gigaflops），但超过硬件缓存容量后效率增速放缓，且显存占用增加（可能导致内存溢出）。
    • 平衡策略：选择 b 使得计算效率接近峰值（如 GPU 常用 128-1024），同时避免过大导致梯度过稳（可能错过最优解）。

小批量 SGD 与梯度下降、随机梯度下降的核心区别是什么？

算法每次迭代数据量梯度计算成本梯度方差硬件利用率
梯度下降全量数据（n）O(n)0低（全量数据可能超出缓存）
随机梯度下降单样本（1）O(1)高低（单样本无法向量化）
小批量 SGD小批量（b）O(b)中（σ/√b）高（向量化+缓存优化）
  • 核心区别：小批量 SGD 通过折中数据量（b），在计算成本（O(b)）、梯度方差（中等）和硬件利用率（高）之间取得平衡，是深度学习中最常用的优化方法。

动量法​

动量法核心原理​

  1. 泄漏平均值（Leaky Average）
    • 定义：动量变量v_t为历史梯度的加权和，公式为：$$v_t = \beta v_{t-1} + g_t \quad (\beta \in (0, 1))$$其中g_t为当前小批量梯度，β控制历史梯度的衰减速度（如β=0.5时，当前梯度权重为 50%，前一步梯度权重 25%，依此类推）。
    • 物理意义：模拟物体运动的惯性，当前速度受历史速度和当前力（梯度）影响，平滑更新方向。
  2. 条件不佳的优化问题
    • 问题场景：目标函数在不同方向曲率差异大（如$f(x) = 0.1x1² + 2x2²$），导致梯度下降在陡峭方向（x2）震荡、扁平方向（x1）收敛缓慢。
    • 梯度下降缺陷：
      • 学习率小：x2 方向稳定但 x1 收敛极慢（20 次迭代后 x1=-0.94）。
      • 学习率大：x1 收敛加快，但 x2 方向发散（如η=0.6时 x2=-1673）。
  3. 动量法更新规则
    • 公式：$$v_t = \beta v_{t-1} + g_t, \quad x_t = x_{t-1} - \eta v_t$$
    • 效果：
      • 扁平方向（x1）：梯度方向一致，动量累积加速更新（20 次迭代后 x1≈0.007）。
      • 陡峭方向（x2）：震荡梯度相互抵消，减少步长波动（x2 从发散转为收敛至 0.0025）。

动量法关键参数与实验验证​

参数作用典型值实验效果（以 f(x)=0.1x1²+2x2² 为例）
动量β控制历史梯度权重，β 越大，历史影响越强0.5-0.9β=0.5：收敛稳定；β=0.25：收敛变慢但优于无动量
学习率η控制更新步长0.001-0.1η=0.6+β=0.5：x1/x2 均收敛至接近 0；η过大：可能导致震荡

实现方式​

  1. 从零开始实现

    • 状态初始化：为权重w和偏置b分别创建动量变量v_w, v_b（初始为 0）。

    • 更新函数：

      def sgd_momentum(params, states, hyperparams):
          for p, v in zip(params, states):
              v[:] = hyperparams['momentum'] * v + p.grad  # 动量更新
              p[:] -= hyperparams['lr'] * v  # 参数更新

  2. 框架简洁实现

    • PyTorch 示例：通过torch.optim.SGD设置momentum参数（如momentum=0.9），自动处理动量累积。
    • 效果对比：相比普通 SGD，动量法在相同学习率下损失下降更快（如loss=0.242 vs 普通 SGD 的loss=0.246）。

理论分析与适用场景​

  1. 二次凸函数分析
    • 目标函数：$h(x) = 0.5x⊤Qx + x⊤c + b$（Q 为正定矩阵），最小值点$x* = -Q⁻¹c$。
    • 动量法优势：通过累积梯度，在特征值差异大的矩阵 Q（如狭长椭球）上，减少“之字形”震荡，加速收敛至最小值。
  2. 有效样本权重
    • 动量β等效于对过去1/(1-β)个梯度的加权平均（如β=0.9时，等效 10 个样本平均），平衡近期与历史梯度影响，提升稳定性。

关键问题​

  1. 动量法如何减少梯度震荡？
    • 答案：通过动量变量v_t累积历史梯度，当前更新方向由当前梯度与历史梯度加权平均决定。对于震荡方向（如陡峭的 x2 方向），正负梯度相互抵消，降低瞬时梯度的噪声影响；对于一致方向（如扁平的 x1 方向），同向梯度累积增强更新速度，从而平滑轨迹，避免发散。
  2. 动量参数 β 的取值如何影响优化效果？
    • 答案：
      • β 接近 0（如 0.25）：动量效应弱，接近普通 SGD，对震荡的抑制作用有限，但比无动量收敛更稳定。
      • β 接近 1（如 0.9）：强调历史梯度，适合梯度方向一致的场景（如扁平区域），加速收敛，但可能导致对当前梯度反应迟钝（需配合较小学习率）。
      • 典型取值：0.5-0.9，根据目标函数曲率差异调整（曲率差异大时取较大 β）。
  3. 动量法在实际应用中需要注意哪些问题？
    • 答案：
      • 学习率调整：动量累积会放大有效步长，需适当降低学习率（如从 0.02 降至 0.01），避免震荡。
      • 初始化动量状态：需为每个参数（如 w, b）独立维护动量变量，确保维度匹配。
      • 非凸问题：虽然理论分析基于凸函数，但实践中对非凸问题（如深度学习模型）仍有效，能帮助跳出浅局部最小值。

AdaGrad 算法​

问题背景：稀疏特征与学习率困境​

  1. 稀疏特征挑战
    • 场景：自然语言处理（如低频词）、计算广告（稀疏用户行为）、协同过滤（稀疏交互数据）。
    • 问题：常见特征（如高频词“学习”）的参数因频繁更新导致学习率过早下降，而稀疏特征（如低频词“预先条件”）的参数因更新次数少，学习率可能已衰减至无法有效更新。
  2. 传统方法局限
    • 固定学习率或全局衰减学习率（如$η=η0/t$）无法针对单个参数的更新频率和梯度大小动态调整，导致“常见特征过拟合，稀疏特征欠拟合”。

AdaGrad 核心算法：自适应学习率机制​

步骤公式/描述
梯度平方累积$s_t = s_{t-1} + g_t²$（逐坐标累加，初始s_0=0），记录历史梯度的平方和。
参数更新$w_t = w_{t-1} - η/(√s_t + ε)·g_t$（$ε=1e-6$防止除零，逐坐标应用）。
学习率调整单个参数的学习率为$η/√s_t$，梯度频繁更新的参数（$s_t$大）学习率低，反之则高。
稀疏特征友好：稀疏特征因梯度出现少，s_t小，学习率高，保证有效更新；常见特征s_t大，学习率低，避免过度更新。
预处理效果：等效于对目标函数二次项矩阵Q的对角线进行归一化（Q~_ii=1），改善优化问题的条件数（κ），缓解“峡谷”型目标函数的优化困难。

理论分析：从预处理到收敛性​

  1. 预处理视角
    • 目标函数二次项x⊤Qx可分解为特征值矩阵Λ，AdaGrad 通过累积梯度平方和s_t，近似实现Q对角线归一化，使各维度梯度规模一致，降低条件数κ=Λ1/Λd。
  2. 收敛性保证
    • 凸问题：学习率按O(t^-1/2)衰减，保证收敛至最优解；
    • 非凸问题：缓解梯度爆炸/消失，提升优化稳定性，但缺乏强理论保证。

关键问题​

  1. AdaGrad 如何解决稀疏特征的优化问题？
    • 答案：通过为每个参数维护独立的梯度平方累积变量s_t，稀疏特征因梯度出现少，s_t小，学习率η/√s_t大，确保有限次数的更新仍能有效调整参数；常见特征因梯度频繁更新，s_t大，学习率自动降低，避免过度调整，平衡了不同特征的优化效率。
  2. AdaGrad 与 SGD 的核心区别是什么？
    • 答案：
      • 学习率机制：SGD 使用全局固定学习率，AdaGrad 为每个参数动态自适应学习率（η/√s_t）；
      • 梯度利用：SGD 仅用当前梯度，AdaGrad 累积历史梯度平方和，反映参数更新的频繁程度和梯度规模；
      • 适用场景：SGD 适合均匀特征数据，AdaGrad 擅长稀疏特征场景（如自然语言处理、计算广告）。
  3. AdaGrad 中梯度平方累积s_t的作用是什么？
    • 答案：
      • 调整学习率：s_t越大，说明该参数历史梯度绝对值越大或更新越频繁，学习率η/√s_t越小，抑制过度更新；
      • 预处理代理：作为目标函数 Hessian 矩阵对角线的廉价替代，近似归一化各维度梯度规模，改善优化问题的条件数，使各维度更新更均衡。

RMSProp 算法​

问题背景与核心改进​

  1. Adagrad 的缺陷
    • 学习率衰减过快：通过累加所有历史梯度平方（s_t = s_{t-1} + g_t²），导致s_t无界增长，学习率按O(t^-1/2)单调下降，后期更新极慢（如 20 次迭代后 x1=-2.38）。
    • 非凸问题局限：固定衰减策略不适用于深度学习中的非凸目标函数，可能陷入局部最小值或鞍点。
  2. RMSProp 的改进思路
    • 引入泄漏平均值（动量法思想）：通过参数γ∈(0,1)控制历史梯度的权重，使s_t仅累积近期梯度平方，避免无界增长。
    • 分离学习率调度：学习率η独立控制，不再依赖全局衰减，适应不同优化阶段。

算法核心原理​

模块公式说明
梯度平方累积$s_t = γs_{t-1} + (1-γ)g_t²$指数加权移动平均，近期梯度权重更高（如 γ=0.9 时，当前梯度权重 10%，前一步 9%，依此类推）
参数更新$x_t = x_{t-1} - η / √(s_t + ε) · g_t$（ε=1e-6）按坐标自适应学习率，梯度频繁的参数学习率低，稀疏参数学习率高
γ 参数作用控制历史梯度影响时长，等效平均过去1/(1-γ)步梯度（如 γ=0.9 对应 10 步平均）平衡近期梯度（低 γ）与历史梯度（高 γ），避免学习率骤降

理论分析与优势​

  1. 与 Adagrad 的核心区别
特性AdagradRMSProp
梯度平方累积全历史累加（s_t 线性增长）指数加权平均（s_t 有界）
学习率衰减率O(t^-1/2)由 γ 控制（非单调衰减）
适用场景凸问题、稀疏特征非凸问题、深度学习

  1. γ 参数的关键作用

    • 历史记录时长：γ 越大，历史梯度影响越久（如 γ=0.9 时，前 10 步梯度贡献约 65%，10 步后贡献<5%）。
    • 稳定性与灵活性：低 γ（如 0.7）侧重近期梯度，适合梯度变化剧烈场景；高 γ（如 0.95）适合梯度方向稳定场景。

  2. 核心优势

    • 非凸问题友好：避免学习率过早衰减，允许在优化后期保持有效更新（如实验中 x2 收敛至 0）。
    • 计算高效：仅增加逐坐标梯度平方的加权累积，复杂度与 SGD 相当（O(d) per step）。
    • 稀疏特征优化：保留 Adagrad 的坐标自适应优势，稀疏特征因s_t小而学习率高，更新更有效。

关键问题​

  1. RMSProp 如何解决 Adagrad 学习率衰减过快的问题？
    • 答案：通过引入泄漏平均值γ，将梯度平方和s_t改为指数加权移动平均（s_t = γs_{t-1} + (1-γ)g_t²），避免s_t无界增长。γ 控制历史梯度的权重，使s_t仅累积近期梯度，学习率η/√s_t不再随时间单调递减，而是根据近期梯度动态调整，在非凸问题中保持后期更新能力（如实验中 RMSProp 的 x1 在 20 次迭代后接近 0，而 Adagrad 仍偏离较远）。
  2. γ 参数的取值对 RMSProp 有何影响？
    • 答案：γ 决定了历史梯度的影响时长：
      • γ 接近 1（如 0.9）：等效平均过去约 10 步梯度，适合梯度方向稳定场景，减少噪声影响（如案例中 γ=0.9 时 x2 收敛至 0）；
      • γ 接近 0（如 0.7）：侧重近期梯度（约 3 步平均），适合梯度变化剧烈场景，快速响应当前梯度（如稀疏特征突发更新）。
      • γ=1：退化为 Adagrad（s_t 固定为初始值，失去动态调整能力，导致学习率不变，可能引发震荡或发散）。
  3. RMSProp 在深度学习中的主要优势是什么？
    • 答案：
      • 坐标自适应学习率：继承 Adagrad 的稀疏特征优化优势，对高频更新参数降低学习率，稀疏参数保持高学习率（如自然语言处理中的低频词嵌入）；
      • 非凸问题稳定性：通过 γ 平衡历史与当前梯度，避免陷入浅局部最小值，适合深度学习复杂非凸目标函数（如神经网络损失函数）；
      • 计算效率：仅增加线性复杂度的梯度平方加权累积，适合大规模数据集和深度网络（如实验中每 epoch 耗时仅 0.014 秒）。

Adadelta​

核心改进：无显式学习率的自适应优化​

  1. 针对 AdaGrad 的缺陷
    • AdaGrad 通过累加全历史梯度平方导致学习率单调衰减，后期更新过慢；
    • Adadelta 引入双状态变量，用指数加权移动平均（泄漏平均值）替代全历史累加，避免s_t无界增长，实现动态学习率调整。
  2. 核心思想
    • 无需手动设置学习率η，通过**参数变化量Δx_t**校准梯度缩放，实现“以变化量驱动变化”的自适应优化。

算法原理与公式推导​

模块公式说明
梯度平方累积$s_t = ρs_{t-1} + (1-ρ)g_t²$指数加权平均，近期梯度权重更高（ρ=0.9 时当前梯度权重 10%，前一步 9%）
参数变化累积$Δx_t = ρΔx_{t-1} + (1-ρ)g_t'²$记录调整后梯度的平方，用于后续梯度缩放
调整后梯度$g_t' = (√Δx_{t-1} + ϵ) / (√s_t + ϵ) · g_t$（ϵ=1e-5）通过历史参数变化与当前梯度平方的比值，动态缩放梯度（避免除零加 ϵ）
参数更新$x_t = x_{t-1} - g_t'$直接使用调整后的梯度更新参数，无需显式学习率η

实现步骤与关键参数​

  1. 状态初始化
    • 为每个参数（如权重 w、偏置 b）创建两个状态变量：
      • 梯度平方累积s（初始为 0），参数变化累积Δx（初始为 0）。
  2. 迭代更新逻辑
    1. 更新梯度平方累积：$s = ρ·s_prev + (1-ρ)·g_t²$；
    2. 计算调整后梯度：$g' = (√Δx_prev + ϵ) / (√s + ϵ) · g_t$；
    3. 更新参数：$x = x_prev - g'$；
    4. 更新参数变化累积：$Δx = ρ·Δx_prev + (1-ρ)·g'²$。
  3. 关键参数ρ
    • 取值范围：(0,1)，典型值 0.9（等效平均过去约 10 步数据，半衰期公式：1/(1-ρ)）；
    • 作用：控制历史信息权重，ρ 越大，历史梯度和参数变化的影响越持久（如 ρ=0.9 时，前 10 步贡献约 65%）。

与其他算法的对比​

算法学习率机制梯度累积方式状态变量数量适用场景
AdaGrad全局 η，单调衰减全历史梯度平方累加1 个（s_t）凸问题、稀疏特征
RMSProp显式 η，动态调整梯度平方指数加权平均1 个（s_t）非凸问题、深度学习
Adadelta无显式 η，动态校准梯度+参数变化双累积2 个（s_t, Δx_t）稀疏特征、免调参场景

关键问题​

  1. Adadelta 如何实现“无学习率”优化？
    • 答案：通过两个状态变量动态校准学习率：
      • s_t累积梯度平方的指数加权平均，反映当前梯度的规模；
      • Δx_t累积调整后梯度的平方，代表历史参数变化的规模；
      • 调整后梯度g_t'由两者的平方根比值决定（g_t' ∝ √Δx_prev / √s_t · g_t），等效于用历史变化量自动缩放当前梯度，无需手动设置学习率η。
  2. ρ 参数对 Adadelta 的影响是什么？
    • 答案：ρ 控制历史信息的衰减速度：
      • ρ 接近 1（如 0.9）：等效平均过去约 10 步数据，适合梯度方向稳定场景，减少噪声影响（如案例中 loss 稳定在 0.243）；
      • ρ 接近 0（如 0.5）：仅关注近期 2 步数据，适合梯度剧烈变化场景，快速响应新梯度；
      • 典型取值 0.9：在稳定性和响应速度间平衡，避免学习率骤变。
  3. Adadelta 相比 AdaGrad 的核心优势是什么？
    • 答案：
      • 避免学习率过度衰减：AdaGrad 累加全历史梯度平方，导致s_t无界增长，学习率按O(t^-1/2)单调下降；Adadelta 用指数加权平均限制s_t增长，学习率动态调整，后期仍保持有效更新（如案例中 20 次迭代后 x1 接近 0，而 AdaGrad 的 x1=-2.38）；
      • 减少手动调参：无需设置学习率η，通过参数变化量自动校准，适合快速实验和稀疏特征场景（如自然语言处理中的低频词嵌入）。

Adam 算法​

结合了本章以上算法的优势。

算法原理：融合动量与方差估计的自适应优化​

  1. 核心组成部分
    • 一阶矩（动量）估计：$$v_t = \beta_1 v_{t-1} + (1-\beta_1) g_t \quad (\beta_1=0.9)$$累积历史梯度，平滑更新方向，减少噪声影响（类似动量法）。
    • 二阶矩（方差）估计：$$s_t = \beta_2 s_{t-1} + (1-\beta_2) g_t^2 \quad (\beta_2=0.999)$$累积梯度平方的指数加权平均，动态调整学习率尺度（类似 RMSProp）。
    • 偏差校正：初始化v_0=s_0=0导致初期估计偏差，通过以下公式校正：$$\hat{v}_t = \frac{v_t}{1-\beta_1^t}, \quad \hat{s}_t = \frac{s_t}{1-\beta_2^t}$$ 消除初始阶段的低估问题，提升早期更新稳定性。
  2. 参数更新公式$$g_t' = \eta \frac{\hat{v}_t}{\sqrt{\hat{s}t} + \epsilon}, \quad x_t = x{t-1} - g_t' \quad (\epsilon=1e-6)$$ 通过动量和方差的联合缩放，实现坐标自适应学习率，平衡收敛速度与稳定性。

实现细节与实验验证​

  1. 初始化与状态变量

    • 为每个参数（如w, b）维护两对状态变量：(v_w, s_w), (v_b, s_b)，初始均为 0。
    • 时间步t记录迭代次数，用于偏差校正（t从 1 开始递增）。

  2. 迭代步骤（以 PyTorch 为例）

    def adam(params, states, hyperparams):
        beta1, beta2, eps = 0.9, 0.999, 1e-6
        for p, (v, s) in zip(params, states):
            v[:] = beta1 * v + (1 - beta1) * p.grad
            s[:] = beta2 * s + (1 - beta2) * torch.square(p.grad)
            v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
            s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
            p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr) + eps)
        hyperparams['t'] += 1

Yogi 算法：针对 Adam 的改进​

  1. 问题定位 Adam 的s_t在稀疏梯度或梯度剧烈变化时可能快速增长，导致学习率骤降或发散。
  2. 改进策略
    • 二次矩更新公式：$$s_t = s_{t-1} + (1-\beta_2) g_t^2 \cdot \text{sgn}(g_t^2 - s_{t-1})$$ 通过符号函数sgn控制更新方向，仅当当前梯度平方大于历史估计时才更新，避免s_t无界增长。
    • 优势：减少极端梯度对方差估计的影响，提升非凸问题的稳定性。

关键问题​

  1. Adam 算法相比 RMSProp 和动量法的核心创新是什么？
    • 答案：Adam 融合了动量法的一阶矩估计（平滑梯度方向）和RMSProp 的二阶矩估计（自适应学习率缩放），并通过偏差校正解决初始阶段的估计偏差。相比 RMSProp 仅处理方差，Adam 增加了动量项以加速收敛；相比动量法，Adam 引入方差缩放实现坐标自适应学习率，是二者的结合与改进。
  2. 为什么 Adam 需要进行偏差校正？如何实现？
    • 答案：由于初始状态v_0=s_0=0，前几步的v_t和s_t会显著低估真实动量和方差（如β1=0.9时，t=1 时$v_1=0.1g_1$，而真实平均应为$g_1$）。通过偏差校正公式$v^t = v_t/(1-β1^t)和s^t = s_t/(1-β2^t)$，将初始阶段的指数衰减效应抵消，使早期估计更接近真实值，提升更新稳定性。
  3. Yogi 算法针对 Adam 的主要改进点是什么？在什么场景下效果更好？
    • 答案：Yogi 改进了二次矩s_t的更新方式，引入符号函数sgn(g_t² - s_{t-1})，仅当当前梯度平方大于历史估计时才更新s_t，避免因稀疏梯度或梯度爆炸导致的s_t无界增长。在梯度稀疏且波动大的场景（如自然语言处理中的低频词更新、对抗训练）中，Yogi 能更稳定地控制方差估计，减少发散风险，提升收敛可靠性。

学习率调度器​

学习率调度器的核心价值​

  1. 关键作用
    • 解决固定学习率的缺陷：过大导致优化发散，过小导致收敛缓慢或陷入次优解。
    • 适应优化阶段：初期高学习率快速收敛，后期低学习率精细调整，减少过拟合（如训练损失从 0.179 降至 0.142）。
  2. 核心目标
    • 衰减策略：按$O(t⁻¹/²)$或乘法规则降低学习率，平衡收敛速度与稳定性。
    • 预热机制：初始阶段线性提升学习率，避免随机初始化参数的盲目更新（如前 5 个 epoch 提升稳定性）。

主流调度策略对比​

策略核心公式/机制典型参数优势实验效果（Fashion-MNIST）
单因子调度器乘法衰减：$ηₜ₊₁ = max(η_min, ηₜ·α)$α=0.9, η_min=1e-2简单高效，适合渐进衰减训练损失 0.237，测试 acc 0.883
多因子调度器分段常数衰减：在指定 epoch（如$s={15,30}$）处ηₜ = ηₜ₋₁·αα=0.5, 初始 lr=0.5针对性降低学习率，防止过早停滞测试 acc 从 0.885 提升至 0.904
余弦调度器余弦函数衰减：$ηₜ=η_T+(η₀-η_T)/2·(1+cos(πt/T))$η₀=0.3, η_T=0.01, T=20平滑衰减，适合视觉任务精细优化训练损失 0.142，测试 acc 0.904
预热机制初期线性递增学习率至最大值，再按其他策略衰减预热 5 epoch，线性递增至 0.3防止随机初始化发散，提升早期稳定性前 5 epoch 收敛更平稳，最终 acc 提升

最佳实践建议​

  1. 策略选择
    • 稀疏数据/凸问题：优先单因子或多因子调度器。
    • 视觉/非凸问题：尝试余弦调度器，结合预热机制提升初始化稳定性。
    • 过拟合场景：后期降低学习率，减少参数波动（如多因子调度器在 15/30 epoch 减半）。
  2. 参数调优
    • 初始学习率η₀：通过网格搜索确定，典型值 0.1-0.3（如实验中η₀=0.3效果最佳）。
    • 衰减因子α：0.5-0.9，小值（0.5）适合快速衰减，大值（0.9）适合缓慢调整。

关键问题​

  1. 为什么学习率调度器能减少过拟合？
    • 答案：通过动态降低学习率，后期更新步长减小，参数在最小值附近波动更小，避免过度调整导致的模型复杂度上升。例如，多因子调度器使训练-测试准确率差从 0.053 降至 0.043，过拟合程度减轻。
  2. 余弦调度器相比其他策略的独特优势是什么？
    • 答案：余弦调度器通过余弦函数平滑衰减学习率，初期允许较大步长快速收敛，后期以较小步长精细调整，尤其适合计算机视觉等需要渐进优化的任务。公式ηₜ=η_T+(η₀-η_T)/2·(1+cos(πt/T))确保学习率先降后升再降，平衡全局探索与局部优化，实验中测试准确率达 0.904，高于固定 lr 的 0.879。
  3. 预热机制的核心作用是什么？如何设置预热时长？
    • 答案：预热机制在训练初期线性提升学习率，避免随机初始化参数因高学习率导致的发散，帮助模型先稳定收敛到合理区域再衰减。预热时长通常根据模型复杂度设置，简单模型 5-10 epoch，复杂模型（如深层网络）10-20 epoch，实验中 5 epoch 预热使前 5 轮训练损失下降更平稳，最终测试准确率提升 1-2%。

第十二章 计算性能​

编译器和解释器​

命令式编程与符号式编程​

特性命令式编程符号式编程
执行方式逐行解释执行，动态更新变量状态先定义计算图，编译后一次性执行
优点易调试（可打印中间变量）、开发便捷编译期优化（内存释放、代码合并）、跨平台部署
缺点Python 解释器开销大，多 GPU 利用率低调试复杂，需预先定义完整流程
示例直接调用fancy_func(1,2,3,4)并存储中间变量e,f,g编译整个函数为print((1+2)+(3+4))再执行

混合式编程：融合两种模式的优势​

  • 通过框架提供的编译接口，将命令式定义的模型转换为符号式执行，兼顾开发便捷性与运行效率。
  • 典型场景：调试时用命令式，部署时编译为符号式优化性能。
框架混合式关键函数核心机制优势
MXNetHybridSequential+hybridize()将模型转换为符号式计算图，优化内存与计算流程支持动态形状，编译后速度提升 31%
PyTorchtorch.jit.script()将动态图转换为 TorchScript 静态图，支持 JIT 编译保持 Python 语法，兼容 PyTorch 生态
TensorFlowtf.function()自动将 Eager 模式代码转换为计算图，支持 XLA 加速利用 MLIR 中间表示优化大规模矩阵运算
飞桨（Paddle）paddle.jit.to_static()动态图转静态图，支持输入规格定义兼顾动态开发与静态部署

​ 编译模型的好处之一是我们可以将模型及其参数序列化（保存）到磁盘。这允许这些训练好的模型部署到其他设备上，并且还能方便地使用其他前端编程语言。

异步计算​

Python 是单线程的。MXNet 和 TensorFlow 之类则采用了一种异步编程（asynchronous programming）模型来提高性能，而 PyTorch 则使用了 Python 自己的调度器来实现不同的性能权衡。对 PyTorch 来说 GPU 操作在默认情况下是异步的。

异步计算核心机制​

  1. 前端与后端解耦
    • 前端（Python/R/C++）：负责定义计算逻辑，快速发送任务到后端队列，不阻塞主线程。
    • 后端（C++/CUDA）：独立线程池执行任务，支持 CPU/GPU 并行，自动跟踪计算图依赖（如z = x*y + 2的依赖关系）。
  2. 异步操作优势
    • 无阻塞执行：前端发送任务后立即返回，无需等待后端完成，例如 MXNet 执行 10 次矩阵乘法仅需 0.0159 秒（NumPy 需 0.7530 秒）。
    • 设备利用率：充分利用多 GPU/多核 CPU，减少空闲时间（如 PyTorch GPU 矩阵乘法异步执行耗时 0.0013 秒，同步后 0.0049 秒）。

主流框架实现对比​

框架异步核心函数同步方式典型场景性能对比（矩阵乘法 10 次）
MXNetnp.dot()自动异步入队npx.waitall()（全局）、wait_to_read()（单变量）异步 0.0159 秒 vs 同步 1.1715 秒
PyTorchtorch.mm()默认异步（GPU）torch.cuda.synchronize(device)异步 0.0013 秒 vs 同步 0.0049 秒
飞桨paddle.mm()默认异步（GPU）paddle.device.cuda.synchronize()异步 0.0031 秒 vs 同步 0.0051 秒

关键问题​

哪些操作会隐式触发异步计算的同步，导致性能下降？

  • 答案：
    • 数据转换操作：asnumpy()（MXNet/PyTorch）、item()（标量提取）；
    • 输出操作：print(z)（需等待变量就绪）；
    • 调试工具：Python 调试器断点会强制同步。 这些操作会阻塞前端，迫使后端立即计算，破坏异步优化（如 MXNet 标量转换耗时增加 2 倍）。

自动并行​

核心机制：自动并行化与设备调度​

计算图驱动的任务调度

  • 深度学习框架（MXNet/PyTorch/飞桨）后端自动构建计算图，识别无依赖任务（如不同 GPU 上的矩阵乘法），并行执行以减少总耗时。
  • 关键优势：无需手动编写并行代码，框架自动分配设备资源，提升多 GPU/CPU 利用率。

多 GPU 并行计算实验对比​

框架单 GPU 耗时（秒）双 GPU 并行耗时（秒）加速比（单 GPU 总和/并行）
MXNetGPU1: 0.5143, GPU2: 0.50750.58861.73x（0.5143+0.5075=1.0218/0.5886）
PyTorchGPU1: 0.4600, GPU2: 0.47060.45802.04x（0.46+0.4706=0.9306/0.4580）
飞桨GPU1: 0.9359, GPU2: 0.93690.94391.98x（0.9359+0.9369=1.8728/0.9439）
  • 结论：双 GPU 并行耗时均小于单 GPU 耗时之和，MXNet 加速比 1.73x，PyTorch 达 2.04x，飞桨 1.98x，证明框架有效利用设备并行。

计算与通信并行化：减少数据移动开销​

  1. 场景：GPU 计算后数据复制到 CPU
    • 顺序执行：计算完成后同步复制，耗时=计算时间+传输时间（如 MXNet：0.6960+6.7376=7.4336 秒）。
    • 并行执行：计算与传输重叠（如 PyTorch 设置non_blocking=True），总耗时降至 1.7703 秒，较顺序执行减少 76%。
  2. 关键函数与参数
    • MXNet：npx.waitall()强制同步，copyto(npx.cpu())触发数据传输。
    • PyTorch：to('cpu', non_blocking=True)异步传输，避免等待计算完成。
    • 飞桨：paddle.to_tensor(place=paddle.CPUPlace())同步传输，synchronize()控制设备同步。

关键问题​

  1. 为什么双 GPU 并行计算的总耗时小于单 GPU 耗时之和？
    • 答案：深度学习框架通过计算图分析任务依赖，无依赖的矩阵乘法可在两个 GPU 上同时执行，设备资源独立利用，无需等待对方完成，因此总耗时接近单设备最长任务时间（如 MXNet 双 GPU 耗时 0.5886 秒，接近单 GPU 的 0.5143 秒，而非两者相加）。
  2. 如何利用异步通信减少计算与数据传输的总耗时？
    • 答案：通过设置non_blocking=True（PyTorch）或框架自动调度，在 GPU 计算未完成时提前启动数据传输，利用 PCI-Express 总线与计算并行。例如，PyTorch 中计算与传输并行使总耗时从 2.8112 秒（顺序）降至 1.7703 秒，减少因等待导致的空闲时间。
  3. 不同框架的自动并行化在同步机制上有何差异？
    • 答案：
      • MXNet：通过npx.waitall()全局同步所有设备，wait_to_read()单变量同步；
      • PyTorch：torch.cuda.synchronize(device)按设备同步，默认 GPU 操作异步；
      • 飞桨：paddle.device.cuda.synchronize()控制设备同步，动态图默认异步执行。 差异在于同步粒度（全局/设备级）和默认行为，PyTorch 与飞桨更灵活，MXNet 同步控制更精细。

硬件​

核心硬件组件与特性​

  1. CPU（中央处理器）

    • 缓存层次：
      • L1 缓存：32-64KB，访问延迟1-1.5ns，速度接近时钟周期，分数据/指令缓存。
      • L2 缓存：256-512KB/核心，延迟5ns，共享或独占。
      • L3 缓存：4-256MB，共享，延迟16-25ns，跨核心访问延迟更高（如远程 CPU socket 访问达 40ns）。
    • 矢量化单元：支持 SIMD（单指令多数据），如 x86 的 AVX2（256 位带宽）、ARM 的 NEON（128 位），单周期处理 8-64 对数据，提升矩阵运算效率。
    • 多核与分支预测：多核心并行执行，分支预测单元减少流水线停滞，错误预测延迟约6ns（15-20 周期）。

  2. GPU（图形处理器）

    • 架构设计：
      • CUDA 核心：数量达数千（如 RTX 2080Ti 有 4352 个），支持并行浮点运算。
      • 张量核（Tensor Core）：优化 4x4/16x16 矩阵运算，支持 FP16/INT8/INT4，吞吐量较传统核心提升数倍（如图灵架构 INT4 吞吐量达 32 倍）。
      • 内存：GDDR6/HBM2，带宽达 400GB/s+（如 V100 的 HBM2 带宽 900GB/s），但容量通常小于 CPU 内存（典型 16-32GB）。

  3. 内存与存储设备

    设备带宽随机访问延迟典型场景
    DDR4 内存40-100GB/s~100ns实时数据交互，存储中间结果
    HDD 硬盘100-200MB/s~8ms低频大容量存储（归档）
    SSD（NVMe）1-8GB/s~120μs（随机）高频数据加载（训练数据读取）
    云存储可配置500μs+（远程）弹性扩展，按需分配 IOPs
    • 关键差异：SSD 的 IOPs（10 万-50 万）比 HDD（~100）高 3 个数量级，顺序读取带宽高 10 倍以上，成为深度学习数据加载的首选。

  4. 网络与总线互连

    • PCIe 总线：主流版本 4.0，单通道带宽 16Gbit/s，16 通道达 32GB/s，延迟 5μs，连接 GPU/SSD/网卡。
    • NVLink：专用 GPU 互连，带宽 300Gbit/s（服务器级），1MB 数据传输仅30μs，比 PCIe 快 2-3 倍。
    • 以太网：1G/10G/100Gbit/s，延迟 500μs（数据中心内），适合分布式训练节点通信。

性能优化策略​

  1. 数据局部性
    • 避免随机内存访问：突发读取（Burst Read）效率比随机读取高 500 倍，内存对齐（64 位边界）减少缓存未命中。
    • 利用缓存层次：将高频数据存入 L1/L2 缓存，减少主存访问（如 L1 命中延迟 1ns，主存访问 100ns）。
  2. 矢量化与并行化
    • CPU：通过 AVX2/NEON 指令实现 SIMD，单周期处理多数据（如 128 位寄存器处理 16 个 8 位整数加法）。
    • GPU：大规模并行计算，张量核加速矩阵乘法（如 4x4 矩阵运算吞吐量提升 16 倍）。
  3. 设备协同与通信
    • 计算与通信重叠：GPU 计算时异步传输数据到 CPU（如 PyTorch 的non_blocking=True），减少总线空闲时间。
    • 多设备并行：双 GPU 矩阵运算耗时约为单 GPU 耗时之和的 50%-70%（如 MXNet 双 GPU 并行耗时 0.5886 秒 vs 单 GPU 0.51+0.50 秒）。
  4. 硬件匹配
    • 数据类型适配：训练用 FP16/FP32 避免数值溢出，推断用 INT8/INT4 提升速度（如图灵 GPU INT8 吞吐量比 FP16 高 2 倍）。
    • 批量处理：增大批量大小，充分利用 GPU 高带宽（如批量大小 64 比 32 提升吞吐量 30%）。

典型延迟与带宽对比​

操作延迟带宽
L1 缓存访问1-1.5ns-
主存突发读取100ns40-100GB/s
SSD 顺序读取（NVMe）208μs4.8GB/s
GPU 全局内存访问200-800ns400GB/s+
PCIe 4.0 x16 传输 1MB80μs12GB/s
NVLink 传输 1MB30μs33GB/s

关键问题​

  1. 为什么 SSD 在深度学习中逐渐取代 HDD？
    • 答案：SSD 的随机访问延迟（120μs）比 HDD（8ms）低 2 个数量级，带宽（1-3GB/s）比 HDD（100-200MB/s）高 10 倍以上，且 IOPs（10 万-50 万）远超 HDD（~100），能快速加载训练数据，减少 CPU/GPU 空闲时间，是高频数据访问的核心存储设备。
  2. GPU 相比 CPU 在矩阵运算上的优势从何而来？
    • 答案：GPU 拥有数千个 CUDA 核心（如 RTX 2080Ti 的 4352 个），支持大规模并行计算；专用张量核优化 FP16/INT8 矩阵运算，吞吐量比 CPU 矢量化单元高数十倍；高带宽内存（GDDR6/HBM2）减少数据传输瓶颈，适合密集型矩阵操作，而 CPU 核心数少且内存带宽较低，更适合逻辑控制与稀疏计算。
  3. 网络互连对分布式训练的影响如何？
    • 答案：网络带宽（如 NVLink 300Gbit/s vs 以太网 10Gbit/s）和延迟（数据中心内 500μs vs 跨地域 150ms）直接影响多节点参数同步效率。低延迟高带宽互连（如 NVLink）允许计算与通信重叠，减少节点等待时间；而以太网等低速网络可能成为瓶颈，导致计算资源闲置，因此分布式训练需优先选择高速互连（如 PCIe/NVLink）并优化通信协议（如 NCCL）。

多 GPU 训练​

多 GPU 训练方法对比​

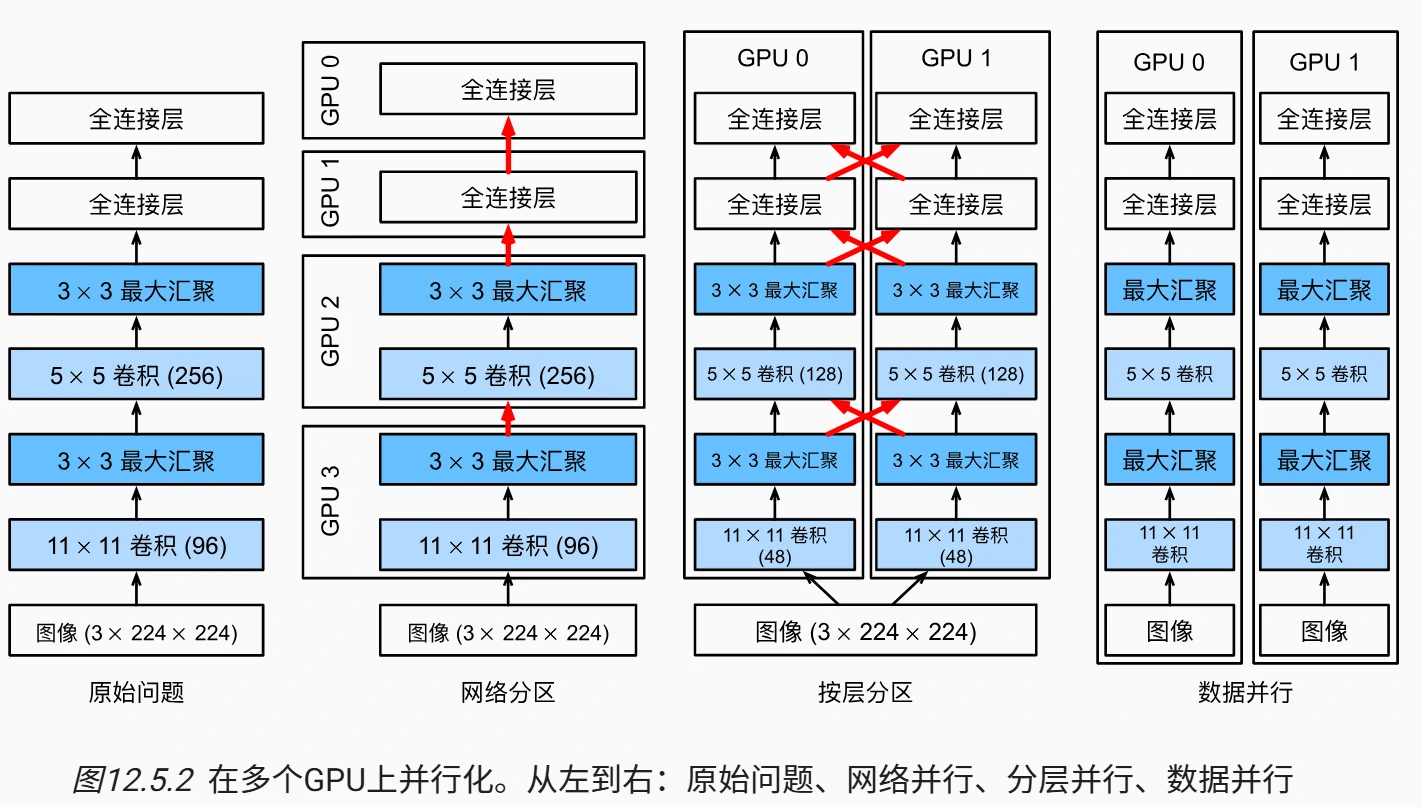
多GPU训练方法对比
方法核心思路优势劣势适用场景
模型并行拆分网络层到不同 GPU（如 GPU1 处理前两层，GPU2 处理后两层）支持更大模型层间同步复杂，数据传输开销大超大模型（显存受限）
层内拆分拆分层内计算（如卷积通道分至不同 GPU）显存线性扩展需严格同步，实现复杂特定层优化
数据并行将小批量数据均分至 GPU，独立计算后聚合梯度简单通用，易实现批量大小需随 GPU 数扩展主流选择

数据并行关键技术​

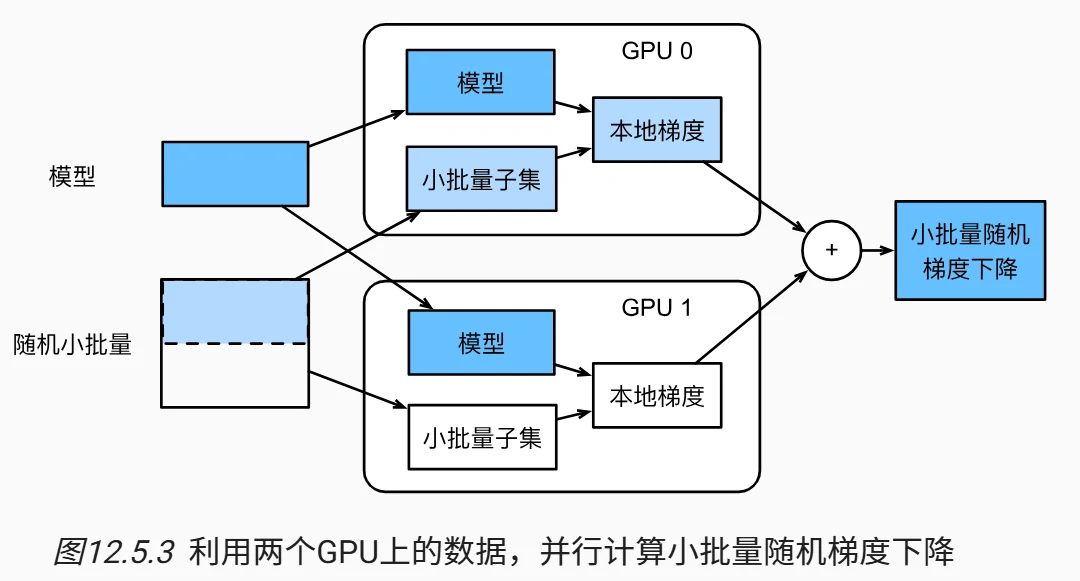
数据并行关键技术流程
  1. 参数分发（get_params） ，数据同步
    • 功能：将模型参数复制到指定 GPU 并启用梯度计算
    • 示例：new_params = get_params(params, d2l.try_gpu(0))，初始化后参数位于 GPU 显存，可独立计算梯度
  2. 梯度聚合（allreduce）
    • 核心逻辑：
      1. 收集各 GPU 梯度并求和（如 GPU0 梯度+GPU1 梯度）
      2. 将聚合结果广播至所有 GPU，确保参数一致性
    • 效率：2GPU 时，2×2 矩阵梯度聚合耗时约 0.01 秒（依赖设备带宽）
  3. 数据拆分（split_batch），数据分发
    • 规则：按 GPU 数量均分数据，如批量大小 256→2GPU 各 128 样本
    • 示例：输入 4×5 矩阵分至 2GPU，各得 2×5 子矩阵

训练流程​

  • 初始化：参数分发至所有 GPU（device_params = [get_params(...) for d in devices]）
  • 前向传播：各 GPU 处理本地数据，计算损失（ls = [loss(...) for ...]）
  • 反向传播：各 GPU 独立计算梯度（l.backward()）
  • 梯度同步：allreduce聚合梯度，确保所有 GPU 参数一致
  • 参数更新：各 GPU 用聚合梯度更新本地参数（sgd函数）

关键问题​

  1. 为什么数据并行是多 GPU 训练的主流选择？
    • 答案：数据并行无需拆分复杂网络结构，仅需将数据均分至 GPU，各设备独立计算梯度后聚合，实现简单且通用，避免模型并行的层间同步开销和显存限制，适合大多数场景（如实验中双 GPU 精度达 0.85，与单 GPU 接近）。
  2. 梯度聚合在数据并行中的作用是什么？
    • 答案：梯度聚合通过allreduce函数将各 GPU 的本地梯度求和并广播，确保所有设备的参数更新一致，避免因数据拆分导致的参数差异。例如，2GPU 分别计算梯度[1,1]和[2,2]，聚合后统一为[3,3]，保证优化方向正确。
  3. 多 GPU 训练时，批量大小和学习率应如何调整？
    • 答案：批量大小需随 GPU 数量线性扩展（如 k GPU 时批量大小 ×k），保持每个 GPU 处理数据量相同；学习率可适当提高（如线性缩放），因更大批量的梯度估计更稳定，可允许更大步长（如原批量 256→512 时，学习率从 0.2→0.4）。

多 GPU 的简洁实现​

核心目标与模型选择​

  • 目标：利用深度学习框架高级 API 简化多 GPU 训练实现，避免手动同步梯度和数据拆分，提升开发效率。
  • 模型：使用修改后的 ResNet-18，特点包括：
    • 输入适配：针对小图像（如 28x28），使用更小的卷积核（3x3）、步长 1、填充 1，移除最大汇聚层。
    • 结构调整：通过残差块（Residual Block）构建，支持 1x1 卷积和步长调整以改变通道数和空间尺寸。

设备配置与参数初始化​

步骤MXNet 实现PyTorch 实现Paddle 实现
获取可用 GPUdevices = d2l.try_all_gpus()devices = [d2l.try_gpu(i) for i in range(n)]同上
参数初始化net.initialize(init=Normal(sigma=0.01), ctx=devices)net.apply(init_weights) + DataParallelnet = DataParallel(net) + 自定义初始化
关键特性上下文列表（ctx）指定设备，参数仅在对应 GPU 初始化自动复制参数到所有设备，支持数据并行类似 PyTorch，通过DataParallel封装

训练流程优化​

  1. 数据拆分与分配

    • 使用split_batch或框架原生函数（如 MXNet 的gluon.utils.split_and_load）将输入数据（如批量大小 512）均分至各 GPU（如 2 个 GPU 各处理 256 样本）。
    • 示例：X_shards, y_shards = split_f(features, labels, devices)。

  2. 并行计算与梯度聚合

    • 前向传播：各 GPU 独立计算梯度，框架自动同步梯度到主设备。
    • 反向传播：损失函数（如 SoftmaxCrossEntropyLoss）在各 GPU 计算后，梯度通过backward()聚合，优化器（如 SGD）统一更新参数。

关键问题​

问题 1：多 GPU 训练中，数据拆分与梯度聚合的核心作用是什么？

  • 数据拆分：将批量数据均分至各 GPU，实现并行计算，提升吞吐量（如 2GPU 处理批量大小 512，等效单 GPU 处理 256×2）。
  • 梯度聚合：各 GPU 计算的梯度同步到主设备，统一更新参数，确保模型权重在所有设备一致，避免训练偏差。

问题 2：若训练时未在指定 GPU 上初始化参数，会出现什么错误？如何避免？

  • 错误：访问参数时会抛出RuntimeError（如“not initialized on cpu”），因参数仅在数据流经的设备上初始化。
  • 避免方法：
    1. 通过net.initialize(ctx=devices)显式在目标设备初始化参数。
    2. 确保训练前至少有一批数据流经所有目标设备，触发自动初始化（框架隐式行为）。

参数服务器​

数据并行训练：梯度聚合策略与硬件瓶颈​

  1. 核心流程

    • 多 GPU 训练中，各设备计算梯度后需聚合到参数服务器，更新后广播回所有设备。
    • 关键步骤：梯度聚合 → 参数更新 → 参数广播，通信效率直接影响训练速度。

  2. 聚合策略性能对比

    • 单 GPU 聚合：3 个 GPU 向第 4 个 GPU 传输 160MB 梯度，每次 10ms（160MB/16GB/s），总耗时 60ms（30ms 传输+30ms 返回）。
    • CPU 聚合：4 个 GPU 向 CPU 传输，总耗时 80ms，因 CPU 通道瓶颈引入 40ms 额外延迟。
    • 分布式聚合：将梯度分 4 块（每块 40MB），各 GPU 并行聚合部分梯度，耗时仅 15ms，利用 PCIe 全带宽。

环同步：高效利用高带宽连接​

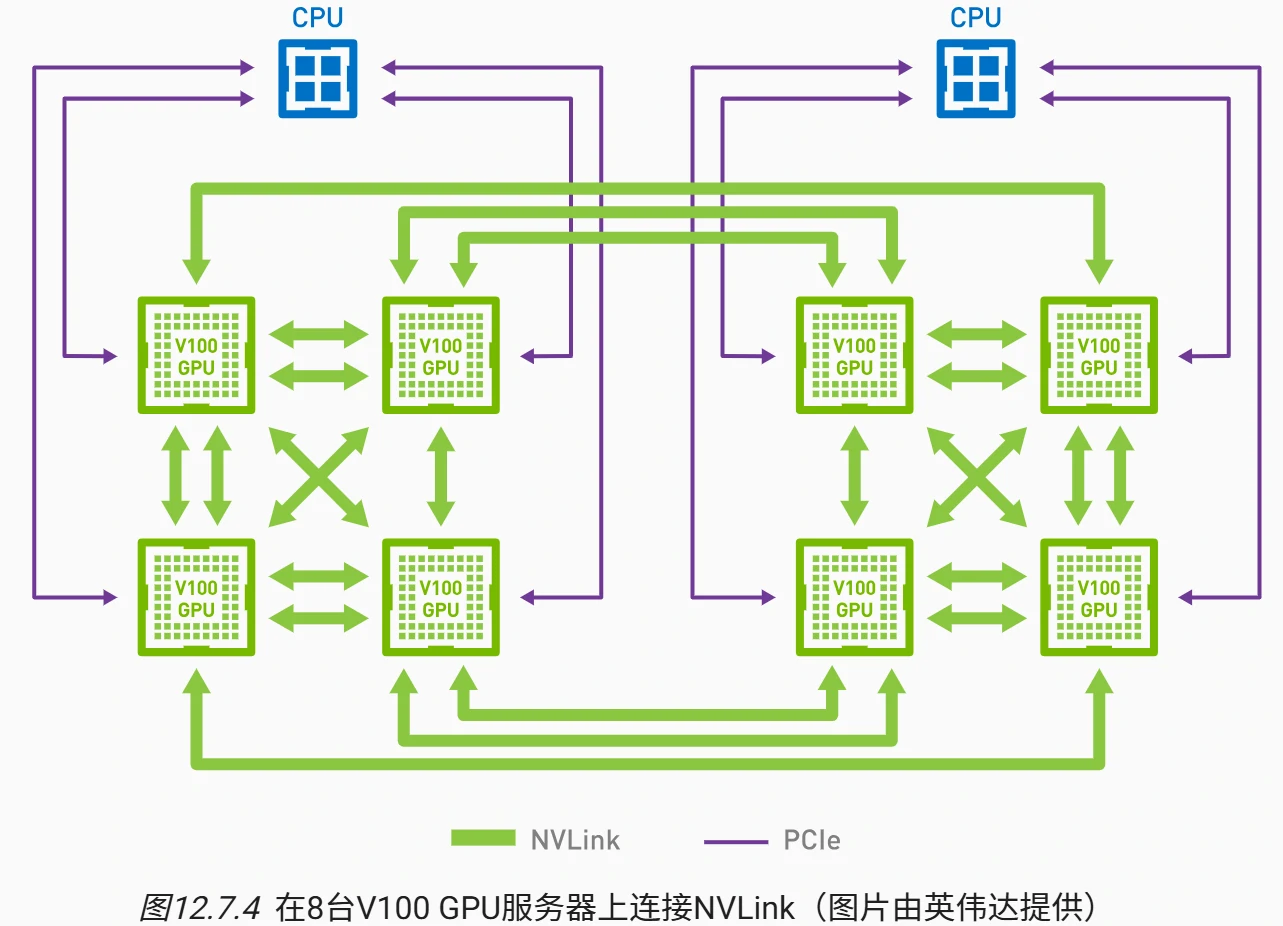
环同步算法结构
  1. 硬件适配场景
    • 针对NVLink 连接的多 GPU 服务器（如 8 卡 V100），每个 GPU 有 6 个 NVLink 接口，双向带宽达 18GB/s/链路。
    • 网络结构分解为双环（高带宽环+常规环），实现梯度分片并行传输。
  2. 核心算法原理
    • 将梯度分为 n 块，节点 i 负责同步第 i 块，通过环结构逐节点传递，最终在 n-1 步内完成聚合。
    • 时间复杂度从线性增长（O(n)）优化为接近常数（如 n=4 时，时间 ≈1 单位）。
  3. 性能数据
    • 8 个 V100 GPU 同步 160MB 梯度： 耗时 ≈2×160MB/(3×18GB/s)≈6ms（双向传输，利用 3 条 NVLink 链路），远优于 PCIe 方案（单 GPU 聚合需 60ms）。

多机训练：分层同步与参数服务器扩展​

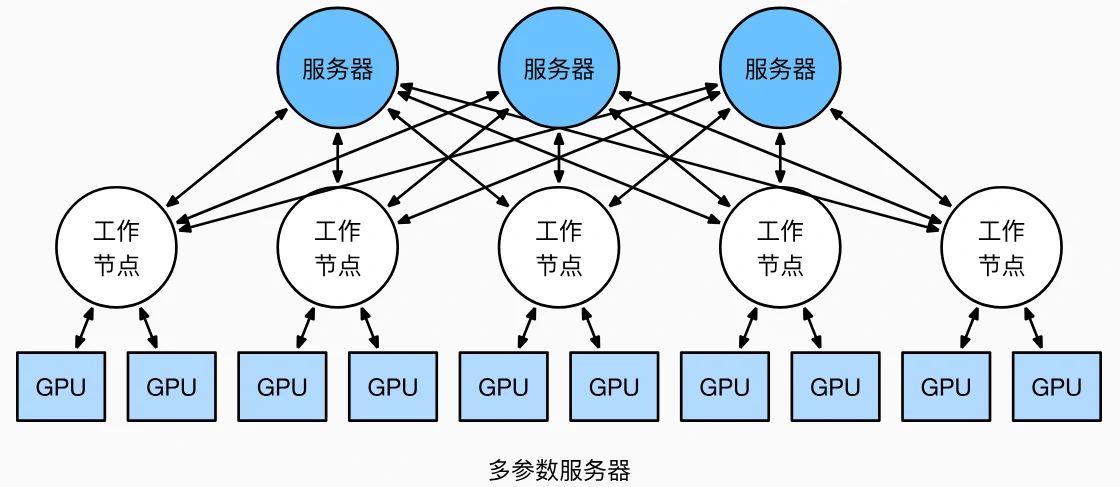
多机训练分层同步架构
  1. 中央服务器瓶颈
    • 单参数服务器架构：m 个工作节点同步时间为 O(m)，带宽受限（如 10GB/s 以太网，m=16 时耗时显著增加）。
  2. 多参数服务器策略
    • 将参数分片存储在 n 个服务器，每个服务器仅处理 1/n 参数，同步时间降至 O(m/n)，实现线性扩展。
    • 分层流程： ① 机器内 GPU 聚合梯度 → 本地 CPU；② 跨机器 CPU 与参数服务器通信；③ 服务器分片聚合后广播更新。

键值存储：抽象化同步操作​

  1. 核心接口
    • Push 操作：工作节点发送梯度（带 key 索引）到公共存储，支持交换归约（如求和），无需控制接收顺序。
    • Pull 操作：获取聚合后的梯度，屏蔽底层网络细节（如环同步、多服务器分片）。
  2. 优势
    • 解耦统计建模（关注梯度计算）与系统工程（处理分布式通信），简化分布式训练开发。
    • 支持异构设备（CPU/GPU）和多节点并行，适配不同硬件架构。

关键问题​

问题 1：为什么环同步在 NVLink 连接的 GPU 集群中效率更高？

答案：NVLink 提供高达 37.5GB/s 的单向带宽（单链路），且每个 GPU 连接多个 NVLink（如 V100 有 6 个）。环同步将梯度分片并行传输，利用双向环结构使每个节点同时发送/接收不同分片，充分利用多链路带宽。例如，8 卡集群中，梯度分 8 块同步，每节点通过 NVLink 并行传输，时间从线性增长转为常数级，相比依赖 PCIe 或 CPU 的集中式聚合，通信时间减少 90%以上。

问题 2：多参数服务器如何解决单服务器带宽瓶颈？

答案：单参数服务器的同步时间随工作节点数 m 呈 O(m)增长，而多参数服务器将参数分片存储（n 个服务器），每个服务器仅处理 1/n 的参数，使总通信量降至 O(m/n)。例如，m=16 个工作节点，n=4 个服务器时，每个服务器只需处理 4 个节点的梯度，同步时间从 O(16)降至 O(4)，有效利用聚合带宽，避免单节点成为瓶颈。

问题 3：键值存储的 Push/Pull 操作如何简化分布式训练？

答案：Push/Pull 操作将复杂的梯度同步逻辑抽象为简单的键值对操作：

  • Push：工作节点无需关心梯度如何聚合（如跨 GPU/机器传输），只需按 key 发送梯度，框架自动处理归约（如求和）。
  • Pull：获取聚合后的参数时，屏蔽底层网络细节（如环结构、分片策略），统计建模者只需关注模型逻辑，系统工程师通过优化键值存储实现高效通信，解耦两者的关注点，降低开发难度。

第十三章 计算机视觉​

图像增广​

核心目标

  • 扩大数据集：通过随机变换生成相似但不同的样本，缓解数据不足问题。
  • 提升泛化能力：减少模型对图像特定属性（如对象位置、颜色、亮度）的依赖，例如通过随机裁剪使模型适应对象在不同位置和尺度的输入。解决过拟合：通过增加数据多样性，降低模型对训练数据的过拟合风险。

常用图像增广方法及实现​

方法类型具体操作参数范围pytorch 框架接口（示例）
翻转左右翻转（Horizontal Flip）概率 50%RandomHorizontalFlip()
上下翻转（Vertical Flip）概率 50%RandomVerticalFlip()
裁剪随机裁剪并 Resize裁剪面积占原图 10%-100%，宽高比 0.5-2，输出尺寸如 200×200RandomResizedCrop(size, scale, ratio)
颜色调整亮度调整随机因子 ∈[0.5, 1.5]（原亮度的 50%-150%）ColorJitter(brightness=0.5)
色调调整随机因子 ∈[-0.5, 0.5]ColorJitter(hue=0.5)
综合调整（亮度、对比度、饱和度、色调）各因子独立随机调整，范围 ±50%ColorJitter(...)
组合方法按顺序应用多种增广-Compose([翻转, 裁剪, 颜色调整])

增广应用原则

  • 训练阶段：随机增广（如翻转、随机裁剪）增加数据多样性，缓解过拟合。
  • 预测阶段：禁用随机增广，仅进行确定性变换（如 Resize、ToTensor），确保输出稳定。

关键问题​

问题 1：训练和预测阶段应用图像增广的区别是什么？为什么？​

答案：

  • 训练阶段：应用随机增广（如 50%概率左右翻转、随机裁剪），目的是生成多样样本，扩大数据集，减少过拟合。
  • 预测阶段：禁用随机增广，仅进行确定性变换（如固定尺寸 Resize、转换数据格式），原因是预测需要稳定的输入-输出映射，随机变换会导致同一图像多次输入产生不同输出，无法保证结果一致性。
问题 2：结合多种图像增广方法时，如何平衡变换强度以避免破坏图像语义？​

答案：

  • 参数控制：每种增广方法的变换强度需合理设置，例如裁剪面积不小于 10%原图，避免丢失关键信息；颜色调整因子控制在 ±50%，防止过度失真。
  • 顺序优化：通常先进行几何变换（翻转、裁剪），再进行颜色调整，避免颜色变化影响几何变换的视觉效果。
  • 可视化验证：通过辅助函数（如apply）可视化增广后的样本，确保变换后的图像仍保留对象语义（如猫的轮廓、纹理可识别），避免过度变换导致样本无效。

微调​

技术背景与核心思想​

  1. 问题场景
    • 目标数据集规模较小（如数千张图像），直接训练复杂模型（如 ResNet-18）易过拟合。
    • 源数据集（如 ImageNet，1000 万张图像）预训练模型已学习通用特征（边缘、纹理、形状），可迁移至目标任务。
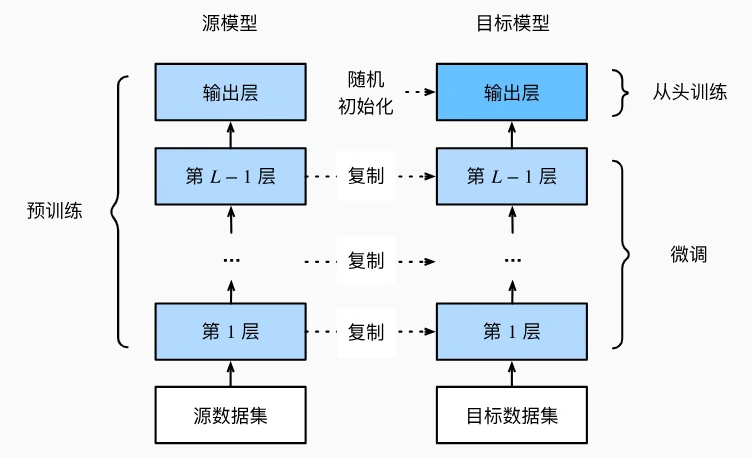
  2. 微调核心逻辑
    • 参数复用：复制源模型除输出层外的所有参数，利用其提取的通用特征。
    • 输出层替换：目标任务类别数通常不同，需重新定义输出层并随机初始化参数。
    • 差异化训练：原有参数通过小学习率微调（避免破坏预训练知识），新输出层通过大学习率从头训练（适配目标任务标签）。
迁移学习微调过程

关键问题​

问题 1：为什么微调时需要对新旧参数设置不同的学习率？​

答案： 旧参数（源模型复制而来）已在大规模数据上学习到通用特征，小学习率微调可避免破坏这些有效特征，仅针对目标任务做细微调整。 新输出层参数随机初始化，需大学习率加速收敛，以快速适配目标任务的少数类别标签，避免因学习率过低导致训练停滞。

问题 2：微调过程中是否可以冻结源模型的所有参数（不更新）？对性能有何影响？​

答案： 可以冻结（即仅训练新输出层），但性能通常低于微调。 冻结参数时，模型仅调整输出层，无法利用目标数据进一步优化特征提取层，可能导致特征与目标任务匹配度不足。案例中若冻结旧层，测试精度可能下降（如从 93.1%降至 90%以下），因源模型特征可能包含与目标任务无关的噪声（如 ImageNet 中的动物特征对热狗识别非必需）。

目标检测和边界框​

目标检测核心目标：识别图像中多个目标的类别和空间位置，与图像分类（仅需分类）形成对比。

边界框表示方法​

表示方法参数定义优势应用场景
两角表示法左上角坐标(x1, y1)、右下角坐标(x2, y2)直观易懂，标注方便人工标注、可视化展示
中心表示法中心坐标(cx, cy)、宽度 w、高度 h便于计算（如锚框生成）算法内部处理（如目标检测模型）

坐标转换函数实现​

  1. 两角转中心（box_corner_to_center）

    • 输入：形状为(n, 4)的张量，每行表示一个边界框的(x1,y1,x2,y2)

    • 计算逻辑： $cx = (x1 + x2) / 2, cy = (y1 + y2) / 2, w = x2 - x1, h = y2 - y1$

    • 输出：形状为(n, 4)的张量，每行表示(cx, cy, w, h)

  2. 中心转两角（box_center_to_corner）

  • 输入：形状为(n, 4)的张量，每行表示(cx, cy, w, h)
  • 计算逻辑： $x1 = cx - w/2, y1 = cy - h/2, x2 = cx + w/2, y2 = cy + h/2$
  • 输出：形状为(n, 4)的张量，每行表示(x1,y1,x2,y2)

边界框标注与可视化​

可视化函数：bbox_to_rect(bbox, color)将边界框转换为 Matplotlib 的矩形对象，支持设置边框颜色（如狗用蓝色，猫用红色），绘制后可直观展示目标位置。

关键问题​

问题 1：目标检测与图像分类的核心区别是什么？​

答案： 图像分类仅需判断图像中主要物体的类别，而目标检测需同时确定图像中多个物体的类别和空间位置（用边界框表示）。 目标检测的输出是包含类别标签和边界框坐标的列表，而图像分类的输出是单一类别概率。

问题 2：为什么边界框的两种表示法需要相互转换？​

答案： 应用场景差异：两角表示法便于人工标注和可视化（直观显示矩形范围），中心表示法便于算法内部计算（如锚框生成、坐标偏移回归）。 算法需求：目标检测模型（如 YOLO、Faster R-CNN）通常在训练时使用中心表示法计算边界框偏移，预测时转换为两角表示法进行可视化，因此需要高效的转换函数支持。

问题 3：边界框转换函数的输入参数为什么要求最内层维度为 4？​

答案： 每个边界框需要 4 个参数唯一确定：

  • 两角表示法：(x1, y1, x2, y2)，分别对应左上角和右下角坐标；

  • 中心表示法：(cx, cy, w, h)，分别对应中心坐标、宽度、高度。

  • 函数设计为处理批量边界框（形状为(n, 4)的张量），其中n为边界框数量，4是每个边界框的固定参数个数，确保输入输出格式统一，便于矩阵运算和批量处理。

锚框​

锚框的核心概念​

  1. 定义
    • 锚框是目标检测中以图像每个像素为中心生成的初始候选边界框，用于后续判断是否包含目标并调整边界。
    • 每个锚框由**缩放比（s）和宽高比（r）**决定大小和形状，其中s∈(0,1]控制相对图像的大小，r>0控制宽高比例。
  2. 作用
    • 覆盖图像中可能存在的多尺度、多形状目标，为目标检测模型提供初始候选区域。
    • 通过后续的分类（是否为目标）和回归（调整边界框坐标），逼近真实边界框（ground-truth）。

锚框生成逻辑​

  1. 参数设置
    • 缩放比列表（sizes）：如s1, s2, ..., sn，控制锚框相对图像的大小（通常包含多个尺度，如 0.2、0.5、1.0）。
    • 宽高比列表（ratios）：如r1, r2, ..., rm，控制锚框的宽高比例（如 1:1、2:1、1:2）。
  2. 组合策略
    • 为避免全组合（n×m 种）带来的计算复杂度，实践中采用固定首个缩放比或宽高比的策略，实际组合数为 n + m − 1。
      • 示例：若$s=[s1, s2]$，$r=[r1, r2, r3]$，则组合为$(s1,r1), (s1,r2), (s1,r3), (s2,r1)$，共2+3−1=4种。
  3. 尺寸计算
    • 锚框宽度：$w = h × s × √r$（h 为图像高度，s 为缩放比，r 为宽高比）。
    • 锚框高度：$h_box = h × s / √r$（确保宽高比为$w:h_box = r$）。

交并比​

交并比来衡量锚框和真实边界框之间、以及不同锚框之间的相似度。公式 $\text{J(A,B)} = \frac{|A \cap B|}{|A \cup B|}$

锚框标注​

在训练集中，我们将每个锚框视为一个训练样本。 为了训练目标检测模型，我们需要每个锚框的类别（class）和偏移量（offset）标签，其中前者是与锚框相关的对象的类别，后者是真实边界框相对于锚框的偏移量。 在预测时，我们为每个图像生成多个锚框，预测所有锚框的类别和偏移量，根据预测的偏移量调整它们的位置以获得预测的边界框，最后只输出符合特定条件的预测边界框。

将真实边界框分配给锚框​

如（左）所示，假设矩阵 X 中的最大值为 x23，我们将真实边界框 B3 分配给锚框 A2。 然后，我们丢弃矩阵第 2 行和第 3 列中的所有元素，在剩余元素（阴影区域）中找到最大的 x71，然后将真实边界框 B1 分配给锚框 A7。 接下来，如（中）所示，丢弃矩阵第 7 行和第 1 列中的所有元素，在剩余元素（阴影区域）中找到最大的 x54，然后将真实边界框 B4 分配给锚框 A5。 最后，如 (右）所示，丢弃矩阵第 5 行和第 4 列中的所有元素，在剩余元素（阴影区域）中找到最大的 x92，然后将真实边界框 B2 分配给锚框 A9。 之后，我们只需要遍历剩余的锚框 A1,A3,A4,A6,A8，然后根据交并比阈值确定是否为它们分配真实边界框。

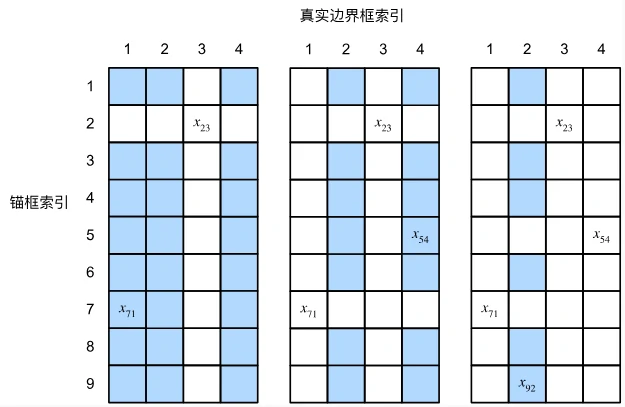
锚框分配标注过程
标记类别和偏移量​

假设一个锚框 A 被分配了一个真实边界框 B。 一方面，锚框 A 的类别将被标记为与 B 相同。 另一方面，锚框 A 的偏移量将根据 B 和 A 中心坐标的相对位置以及这两个框的相对大小进行标记。如果一个锚框没有被分配真实边界框，我们只需将锚框的类别标记为背景。 背景类别的锚框通常被称为负类锚框，其余的被称为正类 锚框。

当有许多锚框时，可能会输出许多相似的具有明显重叠的预测边界框，都围绕着同一目标。 为了简化输出，我们可以使用非极大值抑制（non-maximum suppression，NMS）合并属于同一目标的类似的预测边界框。

以下是非极大值抑制的工作原理。 对于一个预测边界框 B，目标检测模型会计算每个类别的预测概率。 假设最大的预测概率为 p，则该概率所对应的类别 B 即为预测的类别。 具体来说，我们将 p 称为预测边界框 B 的置信度（confidence）。 在同一张图像中，所有预测的非背景边界框都按置信度降序排序，以生成列表 L。然后我们通过以下步骤操作排序列表 L。

  1. 从 L 中选取置信度最高的预测边界框 B1 作为基准，然后将所有与 B1 的 IoU 超过预定阈值 ϵ 的非基准预测边界框从 L 中移除。这时，L 保留了置信度最高的预测边界框，去除了与其太过相似的其他预测边界框。简而言之，那些具有非极大值置信度的边界框被抑制了。
  2. 从 L 中选取置信度第二高的预测边界框 B2 作为又一个基准，然后将所有与 B2 的 IoU 大于 ϵ 的非基准预测边界框从 L 中移除。
  3. 重复上述过程，直到 L 中的所有预测边界框都曾被用作基准。此时，L 中任意一对预测边界框的 IoU 都小于阈值 ϵ；因此，没有一对边界框过于相似。
  4. 输出列表 L 中的所有预测边界框

多尺度目标检测​

多尺度锚框生成策略​

  1. 核心目标
    • 减少锚框数量：通过在不同尺度特征图上采样，避免全像素生成锚框（如 561×728 图像若全像素生成 5 种锚框，总数超 200 万，计算复杂）。
    • 覆盖多尺度目标：小特征图（高分辨率）生成小锚框检测小目标，大特征图（低分辨率）生成大锚框检测大目标。
  2. 生成方法
    • 卷积图层的二维数组输出称为特征图。 通过定义特征图的形状，我们可以确定任何图像上均匀采样锚框的中心。以特征图尺寸（fmap_h, fmap_w）决定锚框中心分布密度，如：
      • 4×4 特征图：生成 16 个均匀分布的锚框中心，适配小目标（锚框尺度s=0.15）。
      • 2×2 特征图：生成 4 个中心，锚框尺度s=0.4，检测中等目标。
      • 1×1 特征图：单一中心，锚框尺度s=0.8，检测大目标。
    • 锚框参数：固定宽高比[1, 2, 0.5]，每个中心生成 3 种形状锚框，平衡形状覆盖性。

多尺度检测原理​

  1. 特征图与感受野关系
    • 浅层特征图（如 CNN 早期层）：分辨率高，感受野小 → 适合检测小目标（如 4×4 特征图对应输入图像局部区域）。
    • 深层特征图（如 CNN 后期层）：分辨率低，感受野大 → 适合检测大目标（如 1×1 特征图对应整个输入图像）。
  2. 检测逻辑
    • 每个特征图空间位置的c个特征单元（通道维度），对应输入图像的同一感受野区域。
    • 利用该区域特征，预测对应中心生成的a个锚框的类别（是否为目标）和偏移量（调整锚框至真实边界框）。
  3. 锚框标记与预测
    • 标记阶段：根据真实边界框，为每个锚框分配类别（目标/背景）和偏移量标签。
    • 预测阶段：模型对每个特征图的锚框输出类别概率和偏移量，通过非极大值抑制（NMS）筛选最终边界框。

关键示例与数据对比​

特征图尺寸锚框尺度（s）锚框中心数量检测目标类型可视化效果
4×40.1516小目标（如宠物细节）锚框密集，无重叠
2×20.44中等目标（如宠物整体）锚框部分重叠
1×10.81大目标（如整只宠物）锚框覆盖整个图像中心

技术优势与核心价值​

  1. 计算效率提升：通过分层采样，锚框数量从全像素的h×w×(n+m−1)降至分层可控（如 3 层共 16+4+1=21 组中心，每组 3 个锚框，总 63 个），减少计算量。
  2. 检测覆盖性增强：多尺度锚框匹配不同大小目标，避免小目标漏检或大目标定位不准。
  3. 分层特征利用：结合 CNN 分层特征（浅层细节、深层语义），提升不同尺度目标的检测精度。

目标检测数据集​

核心用途 用于目标检测模型的快速测试与演示，相比 MNIST 等分类数据集，增加了边界框定位任务。

数据下载与读取实现​

读取函数read_data_bananas

  • 输入参数：is_train区分训练集与验证集。
  • 处理流程：
    • 解析 CSV 文件，提取图像名称和边界框坐标。
    • 读取图像并转换格式，标签坐标**归一化（除以 256）**以适配模型输入。
  • 输出：图像列表（MXNet/PyTorch/Paddle 张量）和标签张量（形状为(n, 1, 5)）。

自定义数据集类与数据加载器​

  1. BananasDataset类
    • 继承：框架数据集类（如 Gluon 的Dataset、PyTorch 的torch.utils.data.Dataset）。
    • 核心方法：
      • __getitem__：返回图像（通道优先，float32）和标签（带批次维度）。
      • __len__：返回数据集大小（训练集 1000，验证集 100）。
    • 打印信息：加载时显示“read X training/validation examples”。
  2. 数据加载器load_data_bananas
    • 功能：创建训练集（shuffle=True）和验证集数据加载器。
    • 批量处理：支持批量大小设置（如batch_size=32），标签不足时用非法边界框（类别-1）填充。

关键问题​

问题 1：香蕉检测数据集与图像分类数据集（如 Fashion-MNIST）的核心区别是什么？​

答案：香蕉检测数据集属于目标检测任务，标签不仅包含类别（索引 0），还包含边界框坐标（左上/右下 x,y），而图像分类数据集（如 Fashion-MNIST）仅包含类别标签。此外，目标检测数据加载需处理边界框的批量填充（非法边界框填充），而分类数据无需此步骤。

问题 2：read_data_bananas函数中标签坐标为何要除以 256？​

答案：图像尺寸统一为 256×256，将边界框坐标除以 256 可实现归一化，使坐标值范围从 0-256 转换为 0-1。这有助于目标检测模型训练时的数值稳定性，避免因坐标绝对值过大导致优化困难，同时统一不同图像的输入尺度。

问题 3：数据加载器中“非法边界框填充”的作用是什么？如何实现？​

答案：

  • 作用：确保同一批量内所有图像的标签具有相同形状。由于不同图像的边界框数量可能不同，填充非法边界框（类别设为-1）使标签形状统一为(batch_size, m, 5)，其中m为最大边界框数（香蕉数据集m=1）。
  • 实现：在BananasDataset中，每张图像仅 1 个边界框，无需额外填充；若数据集包含多边界框，需在数据加载时补全至固定数量，未填充的边界框类别设为-1，坐标设为无效值。

单发多框检测 SSD​

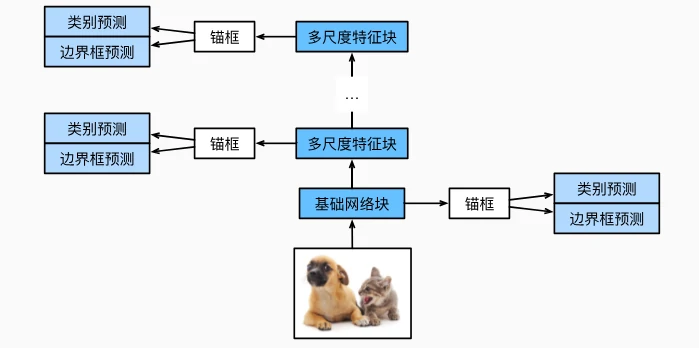
SSD单发多框检测架构

模型架构与核心组件​

  1. 基础网络块

    • 结构：3 个高和宽减半块串联，每个块包含 2 个 3×3 卷积层（padding=1）和 1 个 2×2 最大汇聚层（步幅 2）。
    • 功能：提取图像特征，输出特征图尺寸逐步减半（256→128→64→32），通道数翻倍（16→32→64）。
    • 输出：输入 256×256 图像，输出 32×32 特征图（形状为(batch_size, 64, 32, 32)）。

  2. 多尺度特征块

    • 模块设计：共 5 个模块，块 0 为基础网络，块 1-3 为高和宽减半块（通道数 128），块 4 为全局最大池化（输出 1×1 特征图）。

    • 锚框尺度：

      尺度索引较小值较大值特征图尺寸锚框数量
      00.20.27232×3232²×4=4096
      10.370.44716×1616²×4=1024
      20.540.6198×88²×4=256
      30.710.794×44²×4=64
      40.880.9611×11×4=4
      总计：5444 个锚框/图像。

  3. 预测层实现

    • 类别预测：每个特征图单元生成a个锚框，输出通道数为a×(q+1)（q为目标类别数，香蕉数据集q=1），使用 3×3 卷积保持尺寸不变。
    • 边界框预测：每个锚框预测 4 个偏移量，输出通道数为a×4，同样采用 3×3 卷积。

训练策略与损失函数​

损失函数 将锚框类别和偏移量的损失相加，以获得模型的最终损失函数

  • 类别损失：交叉熵损失，仅计算正类锚框（匹配真实边界框的锚框）和背景类的损失。
  • 偏移量损失：L1 范数损失，通过掩码变量忽略负类和填充锚框，公式为L1(预测偏移量, 真实偏移量) × 掩码。

关键问题​

问题 1：SSD 为什么采用多尺度特征块设计？​

答案：多尺度特征块通过不同大小的特征图生成不同尺度的锚框，匹配目标大小差异：

  • 浅层特征图（如 32×32）分辨率高，感受野小，适合检测小目标；
  • 深层特征图（如 1×1）分辨率低，感受野大，适合检测大目标。 通过 5 个尺度的特征图，SSD 能覆盖从 0.2 到 0.961 比例的目标，提升多尺度目标检测能力。
问题 3：为什么边界框预测使用 L1 损失而非平方损失？​

答案：

  • 鲁棒性：L1 损失对异常值不敏感，避免平方损失因大误差导致梯度爆炸，适合边界框回归任务（存在部分锚框偏移较大的情况）。
  • 计算效率：L1 损失梯度恒定，反向传播时计算更稳定，尤其在多锚框场景下减少优化难度。结合掩码变量，仅正类锚框参与计算，聚焦有效目标的位置回归。

区域卷积神经网络 R-CNN 系列​

R-CNN（2014）​

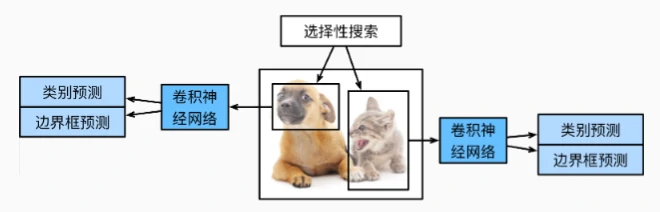
29-R-CNN架构

核心架构

  • 四步流程： ① 选择性搜索生成约 2000 个提议区域（不同尺度、形状），标注真实类别和边界框； ② 预训练 CNN（如 AlexNet）截断至输出层前，将每个区域变形为固定尺寸输入，提取特征； ③ 支持向量机（SVM）分类区域类别（二分类或多分类）； ④ 线性回归模型优化边界框坐标。
  • 缺点：
    • 每个区域独立前向传播，计算冗余（2000 次/图像），速度极慢（47 秒/图像）；
    • 多阶段训练（CNN 预训练+SVM+回归），流程复杂。

Fast R-CNN（2015）​

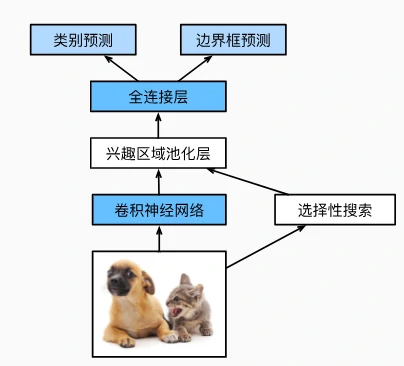
Fast R-CNN架构

核心改进

  • 整图特征共享：

    • 输入整图经 CNN 前向传播，生成全局特征图（如 1×c×h1×w1），避免重复计算；
    • 提议区域（如 2000 个）在特征图上对应兴趣区域，而非原始图像。

  • 兴趣区域汇聚层（RoI 池化）：

    • 将不同形状的兴趣区域（如 3×3、5×5）划分为固定网格（如 2×2），每个子窗口取最大值，输出统一尺寸特征（n×c×h2×w2），便于后续全连接层处理。
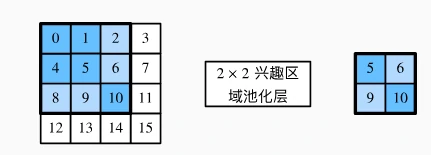
    • 示例：4×4 区域，选取了左上角 3×3 的兴趣区域，经 2×2 RoI 池化，划分为 2×2 子窗口，取各窗口最大值（如 5,6,9,10）。
    RoI池化原理

优势

  • 计算效率提升：仅 1 次整图 CNN 前向传播，耗时从 47 秒 →2.3 秒/图像；
  • 端到端训练：CNN 参数可在检测任务中微调，提升特征针对性。

Faster R-CNN（2015）​

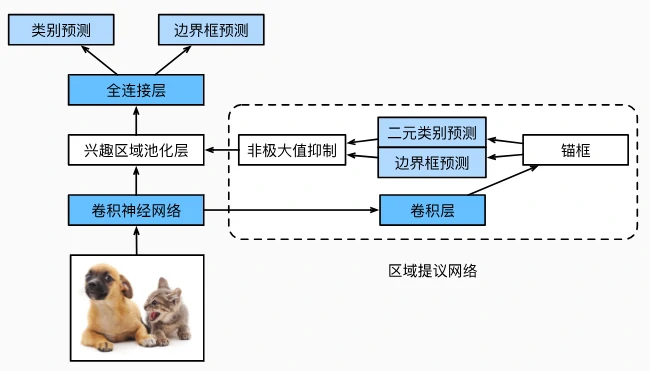
Faster R-CNN架构

区域提议网络（RPN）

  • 替代选择性搜索：
    • 在 CNN 特征图上，每个像素生成多尺度、多宽高比的锚框（类似 SSD），预测锚框的二元类别（目标/背景）和边界框偏移；
    • 非极大值抑制（NMS）筛选高置信度锚框，作为提议区域（约 300 个/图像）。
  • 端到端训练：
    • RPN 与检测网络（分类+回归）联合优化，共享 CNN 特征提取层，生成高质量提议区域；
    • 目标函数包含 RPN 的锚框损失和检测网络的类别/边界框损失。

Mask R-CNN（2017）​

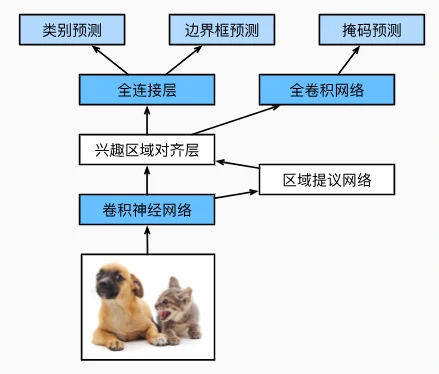
Mask R-CNN架构

像素级预测增强

  • 兴趣区域对齐层：
    • 替代 RoI 池化，使用双线性插值保留特征图空间信息，避免量化误差，更适合像素级分割；
  • 全卷积网络（FCN）：
    • 对每个兴趣区域输出掩码（mask），预测目标像素级轮廓，实现实例分割（同时输出类别、边界框、掩码）。

多任务学习

  • 损失函数包含三部分：类别损失（Softmax）、边界框损失（L1）、掩码损失（二元交叉熵）；
  • 优势：利用像素级标注，在目标检测基础上实现实例分割，精度显著提升（如 COCO 数据集上 AP 提升 10-15%）。

关键问题​

问题 1：为什么 Fast R-CNN 比 R-CNN 速度更快？​

答案：R-CNN 对每个提议区域独立进行 CNN 前向传播（2000 次/图像），计算冗余；而 Fast R-CNN 仅对整图进行 1 次 CNN 前向传播，生成全局特征图，所有提议区域共享特征提取，通过 RoI 池化从特征图中裁剪对应区域，大幅减少计算量（耗时从 47 秒 →2.3 秒/图像）。

问题 2：Faster R-CNN 中的区域提议网络（RPN）解决了什么问题？​

答案：RPN 替代传统的选择性搜索，通过端到端训练生成高质量提议区域：

  1. 高效性：基于 CNN 特征图生成锚框，预测边界框和类别，NMS 筛选后仅保留约 300 个区域，远少于选择性搜索的 2000 个；
  2. 联合优化：RPN 与检测网络共享特征提取层，参数联合训练，使提议区域更贴合检测任务，在减少数量的同时保持精度，避免手动设计的启发式方法。
问题 3：Mask R-CNN 相比 Faster R-CNN 的核心改进是什么？​

答案：Mask R-CNN 在 Faster R-CNN 基础上增加两大模块：

  1. 兴趣区域对齐层：使用双线性插值替代 RoI 池化的取整操作，保留更精确的空间信息，避免特征量化误差，适合像素级预测；
  2. 全卷积网络（FCN）：对每个兴趣区域输出掩码（mask），实现实例分割，即不仅检测目标位置和类别，还预测目标的像素级轮廓，拓展了模型功能至图像分割任务，提升对密集目标和复杂形状的检测精度。

语义分割和数据集​

语义分割任务与数据集概述​

  1. 任务定义

    • 核心目标：将图像每个像素标注为具体语义类别（如“狗”“猫”“背景”），输出像素级分类结果。
    • 与目标检测区别：目标检测输出边界框级类别和位置，语义分割输出像素级类别，标注更精细（如图 13.9.1 中狗的轮廓像素级标注）。

  2. 相关任务对比

    任务类型标注粒度语义区分实例区分典型输出
    语义分割像素级是否每个像素的类别索引矩阵
    目标检测边界框级是否边界框坐标+类别
    实例分割像素级是是每个实例（分类+边界）

  3. Pascal VOC2012 数据集

    • 数据规模：
      • 训练集+验证集：11530 张图像（train.txt含 1464 张，val.txt含 1449 张，实际可用样本经裁剪过滤后减少）。
      • 21 个类别（含背景类），标签为同尺寸 RGB 图像，每个颜色对应唯一类别（如[0,0,0]为背景，[128,0,0]为飞机）。
    • 数据路径：
      • 图像：VOCdevkit/VOC2012/JPEGImages/，格式为.jpg。
      • 标签：VOCdevkit/VOC2012/SegmentationClass/，格式为.webp，颜色值对应VOC_COLORMAP中的类别。

关键技术实现细节​

  1. 标签颜色映射
    • voc_colormap2label函数：构建 RGB 颜色到类别索引的映射，通过三重循环遍历VOC_COLORMAP，将每个颜色值转换为唯一索引（如[128,0,0]→ 索引 1）。
    • voc_label_indices函数：将标签图像的 RGB 值转换为类别索引矩阵，便于模型输入（如输入标签图像尺寸为 H×W，输出同尺寸索引矩阵）。
  2. 裁剪策略对比
    • 随机裁剪 vs 缩放：
      • 缩放可能导致像素错位（如目标边缘模糊），裁剪直接保留原始像素关系，确保语义区域边界清晰，提升分割精度。
      • 示例：输入图像 500×500，裁剪为 320×480，保留中心区域或随机区域，避免缩放引入的变形。

关键问题​

问题 1：语义分割为何采用随机裁剪而非缩放作为预处理方法？​

答案：缩放会改变像素间相对位置，导致语义区域边界模糊（如狗的轮廓经缩放后边缘像素错位），影响模型对精细边界的学习。而随机裁剪直接从原始图像提取固定尺寸区域，保留像素级对齐关系，确保标签与输入图像的语义区域精确对应，尤其对小目标或复杂边界的分割更有利。

问题 2：Pascal VOC2012 数据集的标签如何从 RGB 颜色转换为类别索引？​

答案： 通过voc_colormap2label函数构建映射表：

  1. 定义VOC_COLORMAP列表，包含 21 个类别对应的 RGB 颜色值（如背景为[0,0,0]，索引 0）。
  2. 遍历每个颜色值，计算其唯一索引（如(R*256+G)*256+B），存储到长度为256^3的数组中，索引位置对应颜色值，数组值为类别索引。
  3. 对标签图像的每个像素，通过voc_label_indices函数获取其 RGB 值对应的索引，生成同尺寸的类别索引矩阵。
问题 3：自定义数据集类VOCSegDataset如何处理不同尺寸的输入图像？​

答案：

  1. 过滤机制：在filter方法中，仅保留高度和宽度均不小于裁剪尺寸（如 320×480）的样本，丢弃过小图像。
  2. 随机裁剪：对保留的图像，使用voc_rand_crop函数随机裁剪出固定尺寸区域，确保输入模型的图像和标签尺寸一致（如 320×480），避免缩放带来的信息损失。
  3. 标准化：裁剪后图像转换为浮点型，除以 255 并减去均值、除以标准差，适配模型输入要求（如 ResNet 等预训练模型的标准化参数）。

转置卷积​

核心定义与基本操作​

  1. 转置卷积的本质

    • 目标：通过卷积核“扩张”输入元素，生成尺寸大于输入的输出，用于上采样（如语义分割中恢复特征图尺寸）。

    • 核心机制：对输入每个元素，乘以卷积核后“广播”到中间张量的对应区域，最终累加得到输出。

      • 示例：2×2 输入矩阵 X 与 2×2 卷积核 K，输出为 3×3 矩阵：
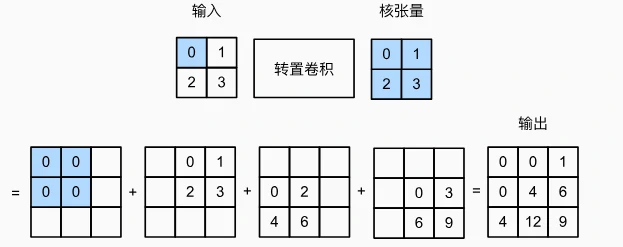
    转置卷积基础操作

  2. 与常规卷积的区别

    • 常规卷积：通过滑动窗口减少空间维度（如 3×3 输入+2×2 卷积核 →2×2 输出）。
    • 转置卷积：通过广播扩展空间维度（如 2×2 输入+2×2 卷积核 →3×3 输出）。

填充，步幅和多通道​

  1. 填充（Padding）

    • 应用对象：作用于输出（常规卷积作用于输入），用于删除输出的边缘行/列。
    • 示例：输入 2×2，卷积核 2×2，padding=1 时，输出从 3×3 缩减为 1×1（删除两侧各 1 行/列）。

  2. 步幅（Stride）

    • 作用：在转置卷积中，步幅被指定为中间结果（输出），而不是输入。控制中间张量的生成间隔，增大步幅会进一步扩大输出尺寸。
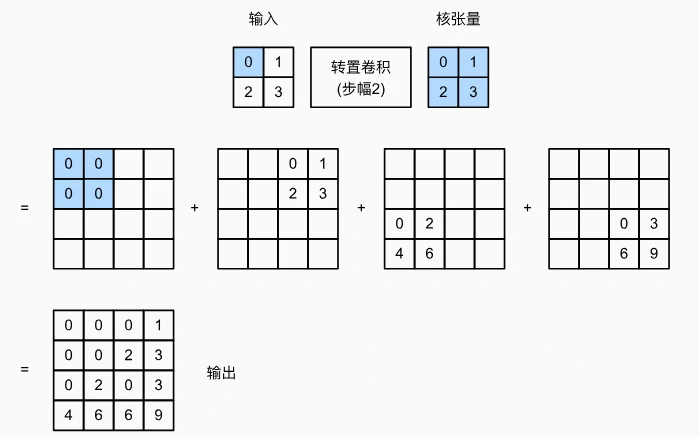
    转置卷积步幅概念

  3. 多通道处理

    • 对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。输入通道数c_in，输出通道数c_out，每个输出通道对应c_in个k_h×k_w的卷积核。

    • 互逆性：若卷积层 f 将 c_in 通道转为 c_out 通道，则转置卷积层 g（参数相同，通道数 c_out→c_in）可恢复输入形状：

      X.shape = (1, 10, 16, 16)
      conv = Conv2D(20, kernel_size=5, padding=2, stride=3)
      tconv = Conv2DTranspose(10, kernel_size=5, padding=2, stride=3)
      tconv(conv(X)).shape == X.shape  # 输出True

矩阵变换与数学本质​

  1. 卷积的矩阵表示
    • 将卷积核展开为稀疏权重矩阵 W（形状为(输出元素数, 输入元素数)），输入向量化后与 W 相乘得到输出。
  2. 转置卷积的矩阵关系
    • 转置卷积等价于权重矩阵转置W⊤与输入向量相乘，实现卷积的反向传播逆运算。
    • 互逆公式：若卷积为y = Wx，则转置卷积为z = W⊤y，满足z ≈ x（忽略填充/步幅时精确恢复）。

核心应用场景​

场景作用
语义分割上采样中间特征图至输入尺寸，实现像素级分类（如 FCN 网络中恢复空间维度）。
图像生成逐步上采样低维特征至高分辨率图像（如 GAN 的生成器中使用转置卷积）。
卷积反向传播作为常规卷积的逆层，传递梯度时交换权重矩阵的正向与反向计算（W⊤替代W）。

全卷积网络​

全卷积网络先使用卷积神经网络抽取图像特征，然后通过 1×1 卷积层将通道数变换为类别个数，最后在通过转置卷积层将特征图的高和宽变换为输入图像的尺寸。 因此，模型输出与输入图像的高和宽相同，且最终输出通道包含了该空间位置像素的类别预测

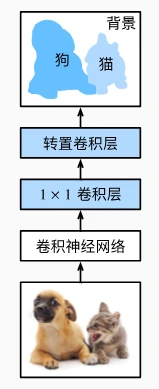
全卷积网络FCN架构

初始化策略​

双线性插值初始化转置卷积

  • 目的：模拟双线性插值上采样效果，提升转置卷积初始参数质量，避免随机初始化导致的模糊。
  • 实现：构造对称核函数，使相邻像素权重随距离递减，公式：$$\text{filt}(i,j) = \left(1 - \frac{|i - \text{center}|}{\text{factor}}\right) \times \left(1 - \frac{|j - \text{center}|}{\text{factor}}\right)$$
  • 效果：输入图像经转置卷积放大 2 倍后，视觉效果接近双线性插值直接放大（如图像边缘平滑）。

数据集与预处理​

数据集Pascal VOC2012
样本规模训练集 1114 例，验证集 1078 例
输入尺寸随机裁剪为 320×480（高宽可被 32 整除，适配转置卷积步幅）
标准化像素值除以 255 后，减去均值[0.485, 0.456, 0.406]，除以标准差[0.229, 0.224, 0.225]
标签格式像素级类别索引（0-20），通过VOC_COLORMAP映射为颜色

训练与预测细节​

  1. 损失函数与优化
    • 损失函数：交叉熵损失（F.cross_entropy），逐像素计算后取平均，忽略通道维。
    • 优化器：SGD，学习率 0.001，权重衰减 5e-4，支持多 GPU 训练（如 2 卡训练速度 254.0 examples/sec）。
  2. 预测流程
    • 输入处理：标准化、通道转换（HWC→CHW）、添加批量维度。
    • 输出处理：对通道维取 argmax，得到像素级类别索引（形状 320×480），通过label2image映射为颜色图像可视化。

关键问题​

问题 1：全卷积网络如何实现像素级分类？​

答案：FCN 通过以下步骤实现像素级分类：

  1. 特征提取：使用 ResNet-18 预训练模型提取特征，保留卷积层，去除全连接层，输出高维特征图（如 320×480 输入 →10×15 特征图）。
  2. 通道转换：1×1 卷积将通道数转为类别数（21 类），每个通道对应一个类别的概率分布。
  3. 尺寸恢复：转置卷积层将特征图放大 32 倍至输入尺寸，每个像素的通道值对应类别概率，通过 argmax 得到最终类别索引，实现像素级一一对应。
问题 2：为什么使用双线性插值初始化转置卷积核？​

答案： 双线性插值是常用的图像上采样方法，能保持图像平滑，避免锯齿边缘。通过初始化转置卷积核为双线性插值核，可使转置卷积在训练初期具备合理的上采样能力，提升模型收敛速度和分割质量。

风格迁移​

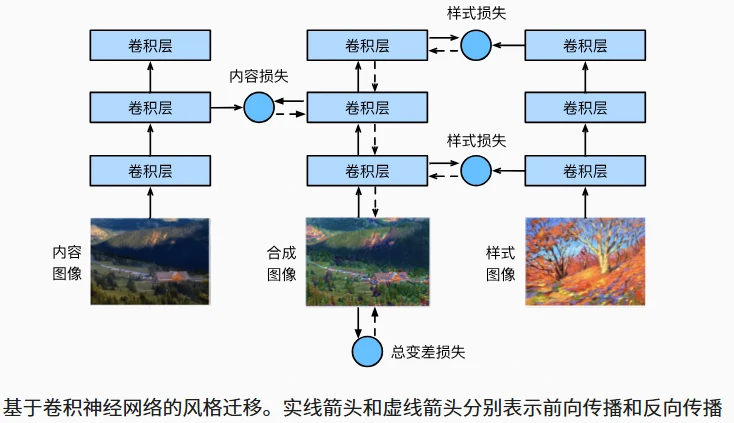
将内容图像的结构与风格图像的纹理/色彩结合，生成视觉上符合风格的合成图像。 我们通过前向传播（实线箭头方向）计算风格迁移的损失函数，并通过反向传播（虚线箭头方向）迭代模型参数，即不断更新合成图像。 风格迁移常用的损失函数由 3 部分组成：

  1. 内容损失使合成图像与内容图像在内容特征上接近；
  2. 风格损失使合成图像与风格图像在风格特征上接近；
  3. 全变分损失则有助于减少合成图像中的噪点。
神经风格迁移流程

数据处理​

  • 标准化： 预处理函数preprocess对输入图像在 RGB 三个通道分别做标准化，并将结果变换成卷积神经网络接受的输入格式。 后处理函数postprocess则将输出图像中的像素值还原回标准化之前的值。 由于图像打印函数要求每个像素的浮点数值在 0 ～ 1 之间，我们对小于 0 和大于 1 的值分别取 0 和 1。。
  • 尺寸调整：统一图像尺寸，确保输入维度一致。

特征提取​

使用基于 ImageNet 数据集预训练的 VGG-19 模型来抽取图像特征。一般来说，越靠近输入层，越容易抽取图像的细节信息；反之，则越容易抽取图像的全局信息。 为了避免合成图像过多保留内容图像的细节，我们选择 VGG 较靠近输出的层，即内容层，来输出图像的内容特征。 我们还从 VGG 中选择不同层的输出来匹配局部和全局的风格，这些图层也称为风格层。

使用 VGG 层抽取特征时，我们只需要用到从输入层到最靠近输出层的内容层或风格层之间的所有层。 构建一个新的网络net，它只保留需要用到的 VGG 的所有层。给定输入X，如果我们简单地调用前向传播net(X)，只能获得最后一层的输出。 由于我们还需要中间层的输出，因此这里我们逐层计算，并保留内容层和风格层的输出。

get_contents函数对内容图像抽取内容特征； get_styles函数对风格图像抽取风格特征。 因为在训练时无须改变预训练的 VGG 的模型参数，所以我们可以在训练开始之前就提取出内容特征和风格特征。 由于合成图像是风格迁移所需迭代的模型参数，我们只能在训练过程中通过调用extract_features函数来抽取合成图像的内容特征和风格特征。

extract_features：逐层计算 VGG 输出，收集内容层与风格层的特征图。

损失函数设计​

损失类型定义公式作用
内容损失合成图像与内容图像在内容层特征的平方误差函数$L_{\text{content}} = \frac{1}{N} \sum (F_{合成} - F_{内容})^2$保留内容图像结构
风格损失合成图像与风格图像在风格层特征的格拉姆矩阵均方误差（格拉姆矩阵表示特征相关性）$L_{\text{style}} = \frac{1}{N} \sum (G_{合成} - G_{风格})^2$，其中$G = \frac{XX^T}{chw}$迁移风格图像的纹理与色彩
全变分损失邻近像素值差异之和，减少高频噪点$L_{\text{TV}} = \sum(x_{i,j} - x_{i+1,j})$去噪点

训练与优化​

  1. 初始化
    • 合成图像初始化为内容图像，作为唯一可学习参数（视为模型参数）。
    • 优化器：Adam，初始学习率 0.9，每 50 个 epoch 衰减 20%（lr_decay_epoch=50）。
  2. 训练循环
    • 前向传播：提取合成图像的内容/风格特征。
    • 反向传播：计算总损失（三部分加权和），更新合成图像像素值。
    • 可视化：每 10 个 epoch 显示合成图像及损失曲线，监控训练进度。

关键实验结果​

  • 合成图像效果：保留内容图像的主体结构（如山脉、树木），同时呈现风格图像的色彩块与笔触纹理（如油画质感）。
  • 损失平衡：通过调整三类损失权重，可控制合成图像偏向内容（增大内容损失权重）或风格（增大风格损失权重）。

关键问题​

问题 1：为什么选择 VGG 网络的不同层提取内容和风格特征？​

答案：

  • 内容特征：选择较深层（如第 25 层），因其捕捉全局语义信息（如物体轮廓、结构），避免合成图像过度保留细节。
  • 风格特征：选择多层（如 0、5、10、19、28 层），低层（如第 0 层）捕捉局部纹理，高层（如第 28 层）捕捉全局风格，多尺度结合更全面迁移风格。
问题 2：格拉姆矩阵在风格损失中的作用是什么？​

答案：

  • 格拉姆矩阵表示特征图中各通道的相关性，反映风格信息（如色彩、纹理的全局分布）。
  • 通过计算合成图像与风格图像的格拉姆矩阵差异，迫使合成图像的特征通道间相关性接近风格图像，从而迁移其风格。
问题 3：全变分损失如何减少合成图像的噪点？​

答案： 全变分损失惩罚相邻像素的剧烈变化，通过最小化$\sum |x_{i,j} - x_{i+1,j}| + |x_{i,j} - x_{i,j+1}|$，使邻近像素值趋于相似，平滑图像，抑制高频噪点（如孤立的亮/暗像素）。

第十四章 自然语言处理：预训练​

词嵌入 word2vec​

  • 将单词映射到固定长度实向量的技术，称为词嵌入，向量可表示单词意义（特征向量）。 word2vec 工具包含两个模型，即跳元模型（skip-gram）和连续词袋（CBOW）。对于在语义上有意义的表示，它们的训练依赖于条件概率，条件概率可以被看作使用语料库中一些词来预测另一些单词。由于是不带标签的数据，因此跳元模型和连续词袋都是自监督模型。
  • 目标：解决独热向量的缺陷，实现词间相似性编码。 将词向量都合并在一起就组成了一个超大的嵌入矩阵

独热向量编码​

One Hot编码

  • 构造：词典大小为$N$，每个词对应长度为$N$的向量，仅索引位置为 1，其余为 0。 （看着就很傻的表示方式）
  • 缺陷：任意两个不同词的独热向量余弦相似度为 0，无法表示词间语义关联（如“猫”和“狗”的相似性）。

word2vec 核心模型​

初始化嵌入矩阵，其中每个词向量都是随机的，然后通过模型进行预测，逐步调整向量，目标是 让 “预测正确” 的总对数概率最大 。

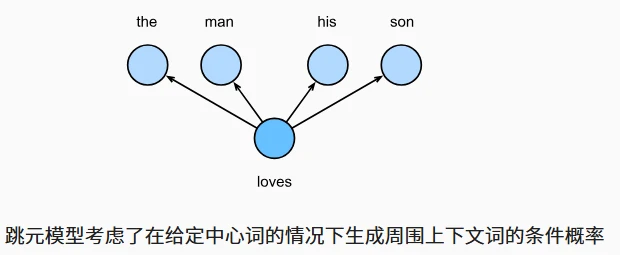
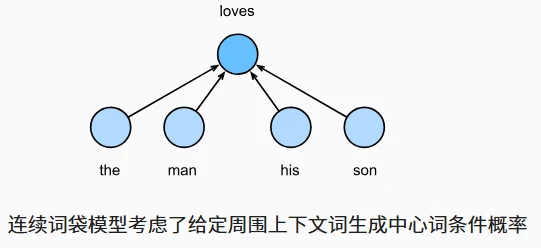
word2vec模型架构 Skip-Gram与CBOW模型对比
对比项跳元模型（Skip-Gram）连续词袋模型（CBOW）
核心假设中心词生成上下文词上下文词生成中心词
条件概率公式$P(w_o \mid w_c) = \frac{\exp(u_o^\top v_c)}{\sum_{i\in V}\exp(u_i^\top v_c)}$$P(w_c\mid w_{o_1},\ldots,w_{o_{2m}})=\frac{\exp\left(\frac{1}{2m}\mathbf{u}c^\top(\mathbf{v}{o_1}+\ldots+\mathbf{v}{o{2m}})\right)}{\sum_{i\in\mathcal{V}}\exp\left(\frac{1}{2m}\mathbf{u}i^\top(\mathbf{v}{o_1}+\ldots+\mathbf{v}{o{2m}})\right)}$
向量作用$v_i$（中心词向量）、$u_i$（上下文词向量）$v_i$（上下文词向量）、$u_i$（中心词向量）
词表示选择中心词向量$v_i$上下文词向量$v_i$
上下文处理方式假设上下文词独立，概率分解为乘积上下文词向量取平均（$\bar{v}o = \frac{v{o1}+\dots+v_{o2m}}{2m}$）
  • 跳元模型适合处理低频词，CBOW 模型对高频词更高效（因上下文词平均减少噪声）。
  • 两者均通过上下文共现关系学习词向量，解决了独热向量的语义缺失问题，成为 NLP 中词表示的基础方法。

训练机制​

  1. 目标函数
    • 均采用极大似然估计，等价于最小化交叉熵损失函数：
      • 跳元模型：$-\sum_{t=1}^T \sum_{-m\leq j\leq m, j\neq0} \log P(w_{t+j}|w_t)$
      • CBOW 模型：$-\sum_{t=1}^T \log P(w_t|w_{t-m},\dots,w_{t-1},w_{t+1},\dots,w_{t+m})$
    • $m$为上下文窗口大小，控制中心词周围考虑的词数（如$m=2$时，左右各 2 个词）。
  2. 梯度计算
    • 跳元模型：对中心词向量$v_c$的梯度为$u_o - \sum_{j\in V} P(w_j|w_c)u_j$，涉及词典所有词的概率加权和。
    • CBOW 模型：对上下文词向量$v_{oi}$的梯度为$\frac{1}{2m}(u_c - \sum_{j\in V} P(w_j|W_o)u_j)$，需计算平均后的梯度。
如何处理“new york”这类由多个单词组成的固定短语的词向量训练？​

答案：根据 word2vec 论文，可通过短语处理技术：

  1. 短语合并：将高频短语（如“new york”）视为单个“合成词”，添加到词典中，分配独立索引。
  2. 子词单元：使用子词切分（如 BPE）将短语拆分为子词，但 word2vec 更常用短语合并，直接处理固定搭配，避免拆分导致的语义损失。
  3. 训练时处理：在文本预处理阶段，通过统计高频共现的连续词，将其合并为短语词，再按普通词进行词向量训练。

近似训练​

在跳元模型和 CBOW 模型中，条件概率计算需对整个词表 V进行 softmax 归一化（如跳元模型的$P(w_o|w_c)=\frac{\exp(u_o^\top v_c)}{\sum_{i\in V}\exp(u_i^\top v_c)}$），导致梯度计算复杂度为O(|V|)。当词表规模达数十万或数百万时，直接计算的成本极高，需近似方法优化--负采样和分层 softmax。

负采样（Negative Sampling）​

  1. 核心原理
    • 将原多分类问题转化为二分类问题：判断词是否为中心词的上下文词（正样本/负样本）。
    • 正样本：上下文窗口内的词，概率用 sigmoid 函数建模：$P(D=1|w_c,w_o)=\sigma(u_o^\top v_c)$，其中$\sigma(x)=\frac{1}{1+\exp(-x)}$。
    • 负样本：从预定义分布$P(w)$（通常基于词频的幂律分布，如$P(w)\propto\text{词频}^{3/4}$）中采样K 个非上下文词，每个负样本的概率为$P(D=0|w_c,w_k)=\sigma(-u_k^\top v_c)$（等价于$1-\sigma(u_k^\top v_c)$）。
  2. 目标函数
    • 对数损失函数为正样本和负样本损失之和：$$-\log\sigma(u_{o}^\top v_c) - \sum_{k=1}^K \log\sigma(-u_{k}^\top v_c)$$
    • 优势：每次计算仅涉及1 个正样本+K 个负样本，复杂度降为O(K)，K 通常取 5-20，远小于|V|。

分层 Softmax（Hierarchical Softmax）​

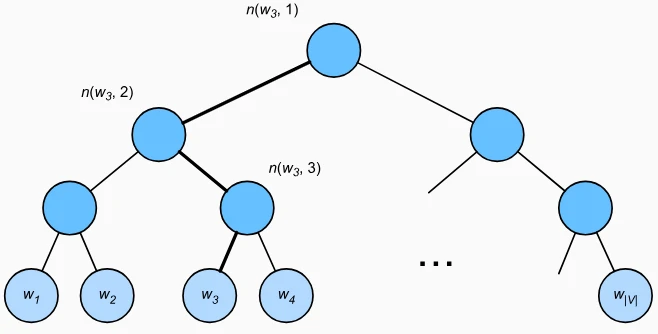
40-分层Softmax

  1. 核心结构
    • 构建一棵二叉树，叶节点对应词表中的每个词，非叶节点为内部节点
    • 每个非叶节点 n 有一个向量$u_n$，用于计算路径上的二分类概率（向左/向右子节点）。
  2. 条件概率计算
    • 从根节点到目标叶节点$w_o$的路径上，每个非叶节点 n(w,j)对应一次二分类决策：$$P(w_o|w_c) = \prod_{j=1}^{L(w_o)-1} \sigma\left([[n(w_o,j+1)\text{是左子节点}]] \cdot u_{n(w_o,j)}^\top v_c\right)$$ 其中$[[x]]=1$（x 为真）或$-1$（x 为假），最终概率为路径上所有二分类概率的乘积。
  3. 计算复杂度
    • 仅需计算路径上的非叶节点数（即树的深度），复杂度为O(log|V|)（假设树为平衡二叉树），远低于原 O(|V|)。
    • 高频词可置于树的浅层（如霍夫曼编码思想），进一步减少平均计算量。

用于预训练词嵌入的数据集​

数据集读取与基础处理​

  1. 数据集选择
    • 使用Penn Tree Bank（PTB），包含来自“华尔街日报”的 42069 个句子，分为训练集、验证集、测试集。
    • 原始数据按行分割，每行是空格分隔的单词，每个单词作为一个词元。
  2. 词表构建 过滤低频词（出现次数<10），未知词用“”表示，最终词表大小为6719。

高频词下采样！​

数据集中的每个词 wi 将有概率地被丢弃。减少“the”“a”等高频词的冗余训练，加速训练并提升有效词的共现信息利用。

公式：对词$w_i$，保留概率为$P(w_i) = \max\left(1 - \sqrt{\frac{t}{f(w_i)}}, 0\right)$，其中$t=10^{-4}$，$f(w_i)$为词频占比。 （高频）词 wi 才能被丢弃，且该词的相对比率越高，被丢弃的概率就越大。

中心词与上下文词提取​

  • 对每个句子中的每个词作为中心词，随机生成 1 到**最大窗口大小（5）**的上下文窗口；
  • 提取窗口内除中心词外的所有词作为上下文词，形成“中心词-上下文词”对。

预训练 word2vec​

数据与模型基础配置​

  1. 数据集与预处理
    • 使用 PTB 数据集，通过 d2l.load_data_ptb 加载，配置参数：
      • 批量大小（batch_size）：512
      • 最大窗口大小（max_window_size）：5
      • 噪声词数量（num_noise_words）：5
    • 词表大小：6719（过滤低频词后），词向量维度（embed_size）设为 100。
  2. 嵌入层定义
    • 模型包含两个嵌入层：
      • net[0]：处理中心词（输入维度=词表大小，输出维度=100），权重记为embed_v；
      • net[1]：处理上下文词和噪声词（输入/输出维度同上），权重记为embed_u。
    • 嵌入层作用：将词元索引映射为稠密向量，如输入索引形状（2,3）对应输出向量形状（2,3,100）。

前向传播与损失函数​

  1. 跳元模型前向传播

    • 函数 skip_gram 实现核心计算：
      • 输入：中心词索引（形状(批量大小, 1)）、上下文-噪声词索引（形状(批量大小, max_len)）；
      • 处理：通过嵌入层获取向量后，使用批量矩阵乘法计算点积，输出形状(批量大小, 1, max_len)，表示中心词与每个上下文/噪声词的关联分数。

  2. 损失函数设计

    • 二元交叉熵损失（SigmoidBCELoss）：

      • 输入：预测分数、标签（1 为正例，0 为负例/填充）、掩码（1 为有效词，0 为填充）；
      • 计算：对有效词的损失求平均，公式为：$$\text{loss} = \frac{1}{\text{有效词数}} \sum (\text{二元交叉熵损失})$$
      • 示例：当预测分数为[1.1, -2.2, 3.3, -4.4]，标签为[1,0,0,0]，掩码为[1,1,1,1]时，损失约为 0.935。

训练过程与参数优化​

  1. 模型初始化与优化器
    • 初始化：两个嵌入层权重随机初始化，设备使用 GPU 加速；
    • 优化器：Adam 优化器，学习率lr=0.002，训练轮次num_epochs=5。
  2. 训练阶段关键步骤
    • 数据加载：从数据迭代器获取 4 个批量数据（中心词、上下文-噪声词、掩码、标签），转换为 GPU 张量；
    • 前向与反向传播：
      1. 通过skip_gram计算预测分数；
      2. 按掩码计算平均损失并反向传播，更新嵌入层权重；

词嵌入应用：相似词检索​

余弦相似度计算

  • 公式：$$\text{cosine sim} = \frac{\mathbf{w}_i \cdot \mathbf{w}_q}{|\mathbf{w}_i| |\mathbf{w}_q|}$$其中$\mathbf{w}_q$为查询词向量，$\mathbf{w}_i$为词表中其他词向量。
  • 实现：使用npx.topk获取 Top-K 相似词索引，排除查询词本身。

关键问题​

问题 1：跳元模型为何需要两个嵌入层？各自的作用是什么？​

答案：跳元模型需要两个嵌入层（embed_v和embed_u）分别处理中心词和上下文/噪声词，原因如下：

  • embed_v：存储中心词的向量表示，用于生成上下文词的条件概率；
  • embed_u：存储上下文词和噪声词的向量表示，在计算点积时作为“被预测词”的特征。 两者权重独立训练，最终通常使用embed_v（中心词向量）作为词嵌入结果，捕捉词的语义信息。
问题 2：如何通过余弦相似度找到语义相似的词？为何需要添加 1e-9 的数值稳定性处理？​

答案： 步骤：

  1. 提取查询词和词表中所有词的向量；
  2. 计算向量点积除以模长乘积，得到余弦相似度（范围[-1,1]，值越大越相似）；
  3. 按相似度排序，选取 Top-K 结果（排除查询词本身）。
  • 数值稳定性：添加1e-9（表示$1 \times 10^{-9}$，即 0.000000001）是为了避免分母为 0 的情况（如向量模长为 0 时），确保除法运算在数值计算中稳定，避免报错或精度损失。

全局变量的词嵌入 GloVe​

利用整个语料库中的统计信息进行词嵌入。

带全局语料统计的跳元模型​

  1. 共现计数定义
    • $x_{ij}$：词$w_i$作为中心词时，词$w_j$在其上下文窗口的共现次数（全局统计），如“ice”与“solid”的共现次数。
    • $x_i = \sum_j x_{ij}$：词$w_i$的上下文词总数，用于计算条件概率$p_{ij} = x_{ij}/x_i$。
  2. 跳元模型损失回顾
    • 原损失：交叉熵$-\sum_i x_i \sum_j p_{ij} \log q_{ij}$，其中$q_{ij} = \frac{\exp(u_j^\top v_i)}{\sum_k \exp(u_k^\top v_i)}$。
    • 问题：softmax 归一化计算昂贵（复杂度$O(|V|)$），罕见事件（低频共现）权重过高。

GloVe 模型核心设计​

三大关键改进​
改进点细节与作用
损失函数替换用平方损失替代交叉熵，直接拟合$\log x_{ij} \approx u_j^\top v_i + b_i + c_j$，避免 softmax 归一化计算。
引入标量偏置添加中心词偏置$b_i$和上下文词偏置$c_j$，捕捉未被向量表示捕获的偏移量，提升拟合精度。
权重函数$h(x_{ij})$控制共现频率的影响： 当$x < 100$时，$h(x) = (x/100)^{0.75}$（低频共现权重递增）；当$x \geq 100$时，$h(x) = 1$（高频共现权重饱和）；$x=0$时权重为 0（忽略未共现词对）。
对称共现特性​
  • 由于上下文窗口对称（词 i 出现在 j 的窗口时，j 也出现在 i 的窗口），$x_{ij} = x_{ji}$，GloVe 拟合对称的$\log x_{ij}$，而 word2vec 拟合非对称的$P(wj|wi)$。
  • 实际应用中，同一词的中心词向量$v_i$和上下文词向量$u_i$会相加作为最终词表示（因初始值不同可能不同，但数学上等价）。
损失函数公式与计算​

  • 目标函数：$$\sum_{i \in V} \sum_{j \in V} h(x_{ij}) \left( u_j^\top v_i + b_i + c_j - \log x_{ij} \right)^2$$

  • 关键参数：

    • $h(x)$：平衡高频/低频共现，避免低频词对损失贡献过小或高频词过度主导。

  • 仅计算$x_{ij} > 0$的词对，提升效率（因$h(0)=0$，零共现词对不参与梯度更新）。

从条件概率比值理解 GloVe​

  1. 共现概率比值的语义价值
    • 例：$p_{ik}/p_{jk}$表示词 k 在 i 和 j 上下文中的相对频率，能区分 i 与 j 的语义差异（如“ice”与“steam”对“solid”和“gas”的共现概率比分别为 8.9 和 0.085，体现语义关联强弱）。
  2. 函数拟合逻辑
    • 假设$\exp(u_j^\top v_i) \approx \alpha p_{ij}$，取对数得$u_j^\top v_i \approx \log \alpha + \log x_{ij} - \log x_i$，通过偏置项$b_i = -\log x_i + \text{常数}$吸收固定项，最终拟合$u_j^\top v_i + b_i + c_j \approx \log x_{ij}$。

与 word2vec 的核心区别​

特性GloVeword2vec（跳元模型）
统计范围全局共现计数（预先计算$x_{ij}$）局部上下文预测（实时生成上下文词）
损失函数平方损失（拟合$\log x_{ij}$）交叉熵（拟合条件概率分布）
对称性对称处理（$x_{ij}=x_{ji}$）非对称处理（$P(wj
计算效率仅计算非零$x_{ij}$，复杂度低softmax 归一化导致高计算成本

关键问题​

问题 1：GloVe 为何引入权重函数$h(x_{ij})$？如何平衡高频与低频共现？​

答案： 目的：避免高频共现词对（如“the”与“a”）主导损失，同时提升低频共现的影响。

  • 平衡机制：
    • 当$x_{ij} < 100$时，$h(x) = (x/100)^{0.75}$，低频共现的权重随频率递增但增速放缓（如 x=10 时权重为 0.316，x=100 时权重为 1）；
    • 当$x_{ij} \geq 100$时，权重固定为 1，防止高频词过度影响损失。
  • 效果：低频共现获得合理权重，高频共现避免“垄断”训练，提升模型对各类共现模式的拟合能力。
问题 2：GloVe 如何利用共现概率比值捕捉词间语义关系？举例说明。​

答案： 核心逻辑：共现概率比值$p_{ik}/p_{jk}$能区分词 i 和 j 的语义差异：

  • 若 k 与 i 相关但与 j 无关（如 k=“solid”，i=“ice”，j=“steam”），比值远大于 1（8.9），说明 i 与 k 更相关；
  • 若 k 与 j 相关但与 i 无关（如 k=“gas”），比值远小于 1（0.085），说明 j 与 k 更相关；
  • 若 k 与 i、j 均相关或均无关（如 k=“water”或“fashion”），比值接近 1，说明语义中立。

模型拟合：通过$\exp(u_j^\top v_i)/\exp(u_k^\top v_i) \approx p_{ij}/p_{ik}$，将比值转化为向量点积的指数形式，从而通过向量运算捕捉语义关系。

问题 3：GloVe 与 word2vec 在处理共现关系上的本质区别是什么？​

答案：

  • 统计层面：
    • GloVe：利用全局预计算的共现计数$x_{ij}$，直接拟合共现对数与向量点积的关系，整合整个语料库的统计信息；
    • word2vec：依赖局部上下文窗口的实时预测，通过条件概率$P(wj|wi)$学习词向量，未显式利用全局统计。
  • 对称性：
    • GloVe：处理对称的共现计数（$x_{ij}=x_{ji}$），词 i 和 j 的共现关系双向等价；
    • word2vec：处理非对称的条件概率（如 P(wi|wj)与 P(wj|wi)独立计算），共现关系单向。
  • 损失函数：
    • GloVe：平方损失，无需 softmax 归一化，计算高效；
    • word2vec：交叉熵损失，需对全词表归一化，大规模词表下计算成本高。

子词嵌入​

在跳元模型和连续词袋模型中，同一词的不同变形形式直接由不同的向量表示，不需要共享参数。为了使用形态信息，fastText 模型提出了一种子词嵌入方法，其中子词是一个字符 n-gram。fastText 可以被认为是子词级跳元模型，而非学习词级向量表示，其中每个中心词由其子词级向量之和表示。

fastText 模型：基于字符 n-gram 的子词嵌入​

  1. 核心原理
    • 子词定义：将单词视为字符 n-gram 的集合，n 范围为 3-6，词首尾添加<和>区分边界（如“where”生成<wh、whe、her、ere、re>、<where>）。
    • 向量表示：单词向量为所有子词向量之和（公式：$v_w = \sum_{g∈G_w} z_g$，$G_w$为单词 w 的子词集合，$z_g$为子词 g 的向量）。
    • 模型结构：基于跳元模型，中心词由子词向量求和表示，其余与跳元模型一致。
  2. 优缺点
    • 优势：
      • 形态捕捉：共享子词参数（如“help”“helps”共享“help”子词），处理词形变化。
      • 泛化能力：未登录词可通过子词组合生成向量（如“unhappiness”拆分为“<un”“unh”等子词）。
    • 不足：
      • 计算成本：每个单词需求和所有子词向量，复杂度随子词数量增加。
      • 词表规模：子词数量多（如 n=3-6 时，英语可能有 3×10⁸ 种 6-元组），模型参数更多。

字节对编码（BPE）：贪心合并生成可变长度子词​

  1. 算法步骤

    • 初始化：

      • 符号表：26 个英文小写字母、词尾符号_、未知符号[UNK]（共 28 个）。
      • 词频统计：将单词转换为符号序列（如“fast*”→“f a s t *”），统计频率（如raw_token_freqs）。

    • 迭代合并（以 10 次合并为例）：

      1. 寻找高频对：通过get_max_freq_pair函数找到当前最频繁的连续符号对（如首次合并“t”和“a”）。

  2. 合并符号：通过merge_symbols函数合并符号对（如“t”+“a”→“ta”），更新符号表和词频（如“t a l l _”→“ta l l _”）。
    3. 重复直至目标词表大小：10 次合并后，符号表新增 10 个符号（如“ta”“tal”“fast_”等）。

  • 单词分割：通过segment_BPE函数按最长匹配原则切分单词（如“tallest*”→“tall e s t *”，未匹配部分用[UNK]表示）。

  1. 关键示例

    • 输入数据：raw_token_freqs = {'fast_':4, 'faster_':3, 'tall_':5, 'taller_':4}。
    • 合并过程：前 3 次合并“t”+“a”→“ta”→“tal”→“tall”，后合并“f”+“a”→“fa”→“fas”→“fast”等。
    • 输出符号表：合并后符号表包含 38 个符号（初始 28+新增 10）。

两种方法对比​

特征fastText字节对编码（BPE）
子词类型固定长度字符 n-gram（n=3-6）可变长度符号对（通过迭代合并生成）
词表大小不固定（依赖 n 范围，可能非常大）可通过合并次数控制（如 10 次合并后新增 10 个符号）
分割方式提取所有可能的 n-gram贪心合并高频符号对，按最长匹配分割
应用场景形态丰富语言（如动词变形）预训练模型输入表示（如 GPT-2、RoBERTa）
未登录词处理通过子词组合表示通过[UNK]和已有子词组合处理
问题 ：字节对编码（BPE）如何确定最佳合并次数？​

答案：BPE 通过贪心策略迭代合并，合并次数由目标词表大小决定。初始符号表大小为 n（如 28），每次合并新增 1 个符号，因此要获得大小为 m 的词表，需执行$m - n$次合并（如从 28 个符号到 38 个需 10 次）。实际应用中，根据任务需求（如模型参数量、处理效率）动态调整合并次数，平衡子词粒度（细粒度如单个字符，粗粒度如完整单词）。

词的相似性和类比任务​

在大型语料库上预先训练的词向量可以应用于下游的自然语言处理任务。

预训练词向量加载​

加载实现 TokenEmbedding类：

  • 功能：下载预训练文件（如.zip），解析.vec文件，构建idx_to_token（索引 → 词）和idx_to_vec（索引 → 向量）映射。
  • 未知词处理：默认索引 0 为<unk>，向量初始化为全 0，未登录词统一用该索引表示。

词相似性任务实现​

  1. 核心算法

    • 余弦相似度：$$\text{cos} = \frac{\mathbf{w}_i \cdot \mathbf{w}_q}{|\mathbf{w}_i| |\mathbf{w}_q|} + 1\text{e-9}$$其中$\mathbf{w}_q$为查询词向量，$\mathbf{w}_i$为词表中词向量，添加1e-9避免分母为 0 的数值不稳定。
    • k 近邻（knn）：通过npx.topk获取相似度最高的 k 个词索引及对应相似度。

  2. 关键函数

    • get_similar_tokens(query_token, k, embed)：
      • 输入：查询词、k 值、预训练嵌入实例（如glove_6b50d）。
      • 输出：排除输入词后的前 k 个相似词及其余弦相似度（保留 3 位小数）。

关键问题​

问题 1：预训练词向量为何能提升词相似性任务的效果？​

答案：预训练词向量（如 GloVe、fastText）在大规模语料库上学习了词汇的语义和语法关系，通过捕捉词共现模式（GloVe）或子词结构（fastText），使语义相近的词在向量空间中距离更近。例如“chip”与“intel”因领域相关性在预训练中频繁共现，向量相似度自然较高，而随机初始化的词向量缺乏这种先验知识。

BERT​

Transformer架构 +双向编码器，没有解码器，输入一个序列，输出一个序列。 对NLP的领域极大贡献就是使得 pre-training+fine-tuning 预训练+微调 模式能够应用起来（计算机视觉领域已经用这个模式很多年了），从此大模型能方便快速应用到很多下游任务，上游专注于模型预训练，模型越来越大。

缝合ELMo与GPT​

  • ELMo：通旧的过双向 LSTM 生成上下文相关表示，但需为每个任务设计特定架构（如拼接 ELMo 向量与 GloVe），灵活性低。
  • GPT：基于 新的Transformer 解码器，但单向编码（左到右），任务无关架构，实现了从特定于任务到不可知任务，但无法捕捉双向依赖（如“bank”依赖右侧“deposit”或“sit down”）。
维度ELMoGPTBERT
编码方向双向（LSTM）单向（Transformer 解码器）双向（Transformer 编码器）
任务相关性需定制架构（拼接特征）任务无关（微调所有参数）任务无关（最小架构更改）
预训练任务双向语言模型单向语言模型MLM + NSP
文本对处理无显式建模无片段嵌入+NSP
代表能力词元级上下文生成式单向上下文词元+句子级双向上下文

双向编码+任务无关架构​

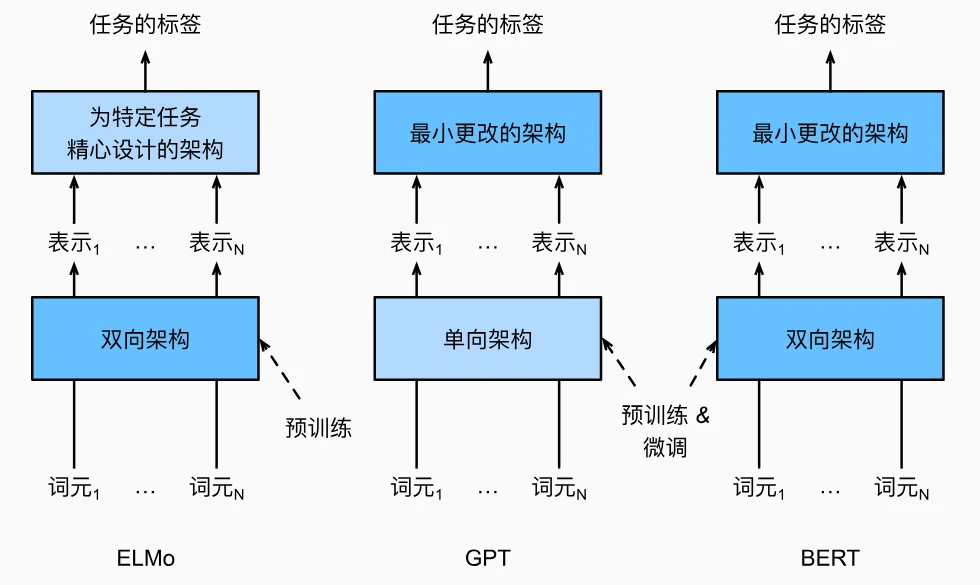
41-BERT双向编码架构.webp

  1. 双向编码能力
    • 采用Transformer 编码器，通过自注意力机制同时关注左右上下文，解决 GPT 单向编码的局限。
    • 示例：“bank”在“deposit cash”和“sit down”中，通过双向上下文分别编码为“银行”和“河岸”的语义。
  2. 输入表示设计
    • 三嵌入融合： 在 Transformer 编码器中常见是，位置嵌入被加入到输入序列的每个位置。然而，与原始的 Transformer 编码器不同，BERT 使用可学习的 位置嵌入。总之，BERT 输入序列的嵌入是词元嵌入、片段嵌入（属于第几个句子）和位置嵌入（句子中位于哪个位置）的和。嵌入层参数都通过学习获得。

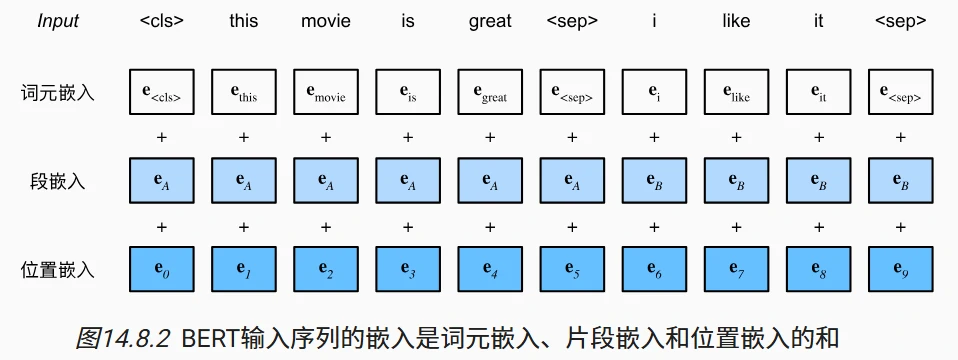
42-BERT输入表示.webp

预训练的两个任务

  • 掩蔽语言模型（MLM）： 学习句子内对词的预测。
    • 策略：随机选择 15%词元作掩蔽（告诉模型要预测这些），其中80%替换为“【MASK】”标记、10%替换为随机词（增加噪音）、10%保留原词（避免微调时未出现【MASK】导致模型难以适应）。
    • 目标：通过双向上下文预测掩蔽词，如“this movie is great”中掩蔽“great”，利用“movie”和“is”预测。
    • 优势：强制模型学习深层语义依赖，提升词元级理解能力。
  • 下一句预测（NSP）： 学习句子间的关系。
    • 数据生成：50%真实连续句（如“句 A 句 B”），50%随机句（如“句 A 句 C”）。
    • 目标：判断两句子是否连续，输出二分类标签，建模文本对逻辑关系（如因果、对比）。
    • 优势：显式捕捉句子级语义关联，提升自然语言推断、问答等任务表现。

数据选择与预处理​

预训练时使用无标号数据，微调时使用有标号数据。输入序列按空格切词，对于不常出现的词，将其分解为子词。 尽量使用较长的文章而不是随机句子。论文中使用了维基百科的25亿数据。WikiText-2：保留原始标点、大小写和数字，适合 NSP 任务的句子关系判断。

BERT 为何采用“80%+10%随机词+10%原词”的掩蔽策略​
  • 避免预训练-微调不匹配：若 100%使用，微调时未见该符号，导致分布差异；
  • 增强模型鲁棒性：10%随机词引入噪声，防止模型依赖“”特殊符号投机预测；
  • 保留真实数据分布：10%保留原词，使模型学习到“非掩蔽时仍需关注上下文”（如“great”在未掩蔽时，模型需通过上下文确认其正确性），增强双向编码的泛化能力。

第十五章 自然语言处理：应用​

情感分析及数据集​

由于情感可以被分类为离散的极性或尺度（例如，积极的和消极的），我们可以将情感分析看作一项文本分类任务，它将可变长度的文本序列转换为固定长度的文本类别。

数据集核心信息​

维度详情
数据集斯坦福 IMDb 大型电影评论数据集，包含25000 条训练评论和25000 条测试评论，正负情感标签各占 50%。
数据来源从 IMDb 下载，存储为文本文件，积极评论存于pos文件夹，消极评论存于neg文件夹。
任务类型二分类任务（积极/消极情感极性判断），属于文本分类问题。

预处理关键步骤​

  1. 数据读取与分词
    • 函数read_imdb：遍历标签文件夹，读取文本内容并去除换行符，标签pos→1，neg→0。
    • 分词方式：按单词分词（d2l.tokenize，token='word'），例如将评论拆分为单词列表。
  2. 词表构建
    • 过滤低频词：仅保留出现次数 ≥5 的单词，生成词表vocab，包含特殊填充符<pad>。
    • 词表规模：依赖训练数据，过滤后词表大小由低频词数量决定。
  3. 序列长度标准化
    • 长度分布：评论长度差异大，通过直方图观察，多数评论长度在 0-800 词元之间（图略）。
    • 截断与填充：使用d2l.truncate_pad将所有评论长度统一为500（不足补<pad>，超长截断），生成特征矩阵(25000, 500)。

数据迭代器配置​

  • 批量大小：64，每次迭代返回一个小批量数据。
  • 输出格式：
    • 特征X：形状为(批量大小, 500)，类型为张量（MXNet/PyTorch/Paddle）。
    • 标签y：形状为(批量大小,)，0 表示消极，1 表示积极。
  • 小批量数目：训练集 391 个（25000 ÷ 64 ≈ 391），测试集同理。

整合函数load_data_imdb​

  • 功能：封装数据集加载全流程，支持指定批量大小和序列长度（默认 500）。

  • 返回值：

    训练数据迭代器（train_iter）

    1. 测试数据迭代器（test_iter）
    2. 词表vocab（包含低频过滤后的单词和特殊符号）。

关键问题​

问题 1：为何要对 IMDb 评论进行截断和填充处理？​

答案： 文本分类模型输入要求固定长度序列，而原始评论长度差异大（直方图显示从几十到近千词元）。 通过截断（超长序列截断）和填充（过短序列补<pad>），将所有评论统一为长度 500，确保批量处理时张量形状一致，便于模型输入和计算。

问题 2：词表构建时过滤低频词（min_freq=5）的目的是什么？​

答案： 低频词（出现次数<5）在训练数据中出现极少，可能为噪声或拼写错误，保留会增加词表规模和模型参数。 过滤后可减少词表大小，提升训练效率，同时避免模型过度拟合罕见词，聚焦高频核心词汇的语义学习。

情感分析：使用循环神经网络​

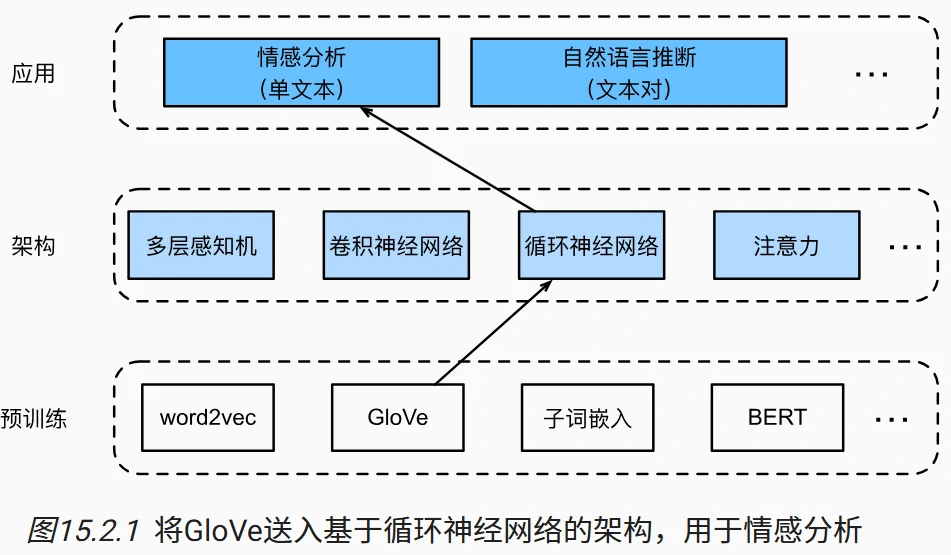
与词相似度和类比任务一样，我们也可以将预先训练的词向量应用于情感分析。由于 IMDb 评论数据集不是很大，使用在大规模语料库上预训练的文本表示可以减少模型的过拟合。我们将使用预训练的 GloVe 模型来表示每个词元，并将这些词元表示送入多层双向循环神经网络以获得文本序列表示，该文本序列表示将被转换为情感分析输出 。

情感分析模型

模型架构设计​

双向循环神经网络（BiRNN）

  • 嵌入层：使用 100 维 GloVe 预训练词向量，冻结参数不参与训练，输入词元索引转换为向量（形状(时间步, 批量大小, 100)）。
  • 编码器：2 层双向 LSTM，隐藏单元 100，输出各时间步隐状态（形状(时间步, 批量大小, 200)，双向合并）。
  • 解码器：全连接层，输入为初始和最终时间步隐状态连结（形状(批量大小, 400)），输出 2 分类 logits。

预训练词向量加载​

  • GloVe 来源：加载“glove.6b.100d”预训练模型，覆盖词表所有词元，向量形状(49346, 100)。
  • 参数冻结：通过net.embedding.weight.requires_grad = False固定嵌入层权重，避免训练中更新。

关键问题​

问题 1：预训练词向量（GloVe）在模型中的作用是什么？​

答案：GloVe 预训练词向量提供基于大规模语料的语义先验知识，如“great”“terrible”等词的初始向量已蕴含情感倾向。在 IMDb 小规模数据集上冻结预训练参数，可避免过拟合，同时减少随机初始化的训练负担，使模型专注于学习序列级情感聚合（如通过 LSTM 编码上下文关系）。

问题 2：模型中为何连结双向 LSTM 的初始和最终时间步隐状态？​

答案：双向 LSTM 的**初始隐状态（正向最后一层）**捕获序列整体语义的“起始特征”，最终隐状态（反向最后一层）捕获序列的“结束特征”，两者连结（4× 隐藏单元数）能**融合双向全局信息，为全连接层提供更全面的文本表示。例如，评论结尾的情感词（如“excellent”）对整体极性判断至关重要，连结操作确保首尾关键信息不丢失。

情感分析：使用卷积神经网络​

只要将任何文本序列想象成一维图像，通过这种方式，一维卷积神经网络可以处理文本中的局部特征，例如 n 元语法。

一维卷积与 textCNN 模型原理​

一维卷积运算

​ 单通道输入：通过滑动窗口计算元素乘积和。 下图中阴影部分 0x1+1x2=2.

一维卷积单通道

​ 多通道输入：各通道独立计算互相关后求和，等价于二维卷积中核高度等于输入高度。

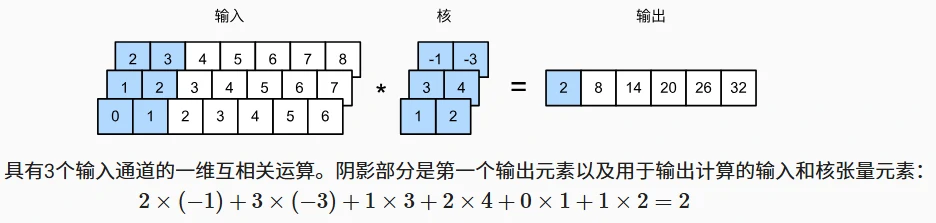
一维卷积多通道

多输入通道的一维互相关等同于单输入通道的二维互相关。

textCNN 架构

46-TextCNN文本分类架构

  • 嵌入层： 双嵌入设计：embedding（可训练，学习任务特定表示）和constant_embedding（固定预训练 GloVe，保留通用语义），输出连结为(批量大小, 词元数, 200)。
  • 卷积层： 多组不同宽度核（如 3、4、5），各 100 输出通道，激活函数 ReLU，捕捉 3-5 元语法特征，输出形状(批量大小, 通道数, 词元数-w+1)。
  • 最大时间汇聚层：对于每个通道在不同时间步存储值的多通道输入，对每个通道取全局最大值，输出(批量大小, 通道数)，连结所有通道形成固定长度特征向量。
  • 全连接层： Dropout（0.5）减少过拟合，线性层输出 2 分类 logits。

关键问题​

问题 1：textCNN 为何使用不同宽度的卷积核？​

答案：不同宽度的卷积核（如 3、4、5）可捕捉不同长度的n 元语法特征：

  • 宽度 3 捕获三元组（如“so great”），宽度 5 捕获五元组（如“absolutely fantastic movie”），覆盖多尺度语义单元。
  • 多组核并行计算，输出经最大时间汇聚后连结，综合不同粒度的局部特征，增强模型对复杂情感表达的捕捉能力。
问题 2：最大时间汇聚层的作用是什么？为何优于平均汇聚？​

答案：

  • 作用：提取每个通道的最大值，保留序列中最显著的局部特征（如情感关键词“terrible”的高激活值），忽略非关键位置的噪声。
  • 优势：相比平均汇聚，最大汇聚对关键情感词更敏感（如“not good”中“good”的负向信号可能被平均弱化，而最大汇聚保留“not”的强否定信号），更适合情感分类的极性判断。
问题 3：textCNN 中双嵌入层的设计目的是什么？​

答案：

  • 固定嵌入层（constant_embedding）：加载预训练 GloVe，保留大规模语料的通用语义（如“excellent”的正向极性），避免随机初始化在小数据集上过拟合。
  • 可训练嵌入层（embedding）：允许模型在训练中调整词向量，学习任务特定表示（如“movie”在影评中的特定情感倾向），平衡预训练知识与任务适配。
  • 连结输出：融合通用与特定特征，扩大特征空间，提升模型对领域特定表达（如电影评论中的“plot”“acting”）的处理能力。

自然语言推断与数据集​

自然语言推断（natural language inference）主要研究 假设（hypothesis）是否可以从前提（premise）中推断出来， 其中两者都是文本序列。 换言之，自然语言推断决定了一对文本序列之间的逻辑关系。

自然语言推断任务定义​

  1. 核心目标：判断两文本序列（前提 vs 假设）的逻辑关系，分为三类：

    • 蕴涵（假设可从前提推出，如“拥抱”→“示爱”）
    • 矛盾（假设的否定可从前提推出，如“运行代码”→“睡觉”）
    • 中性（无法推断，如“表演”→“出名”）

  2. 应用价值：自然语言理解的核心任务，支撑信息检索、问答系统、语义消歧等下游任务。

SNLI 数据集特性​

维度详情
规模训练集 549,367 对，测试集 9,824 对，标签均衡（三类分布接近 1:1:1）。
数据格式每行包含前提、假设、标签（制表符分隔），标签映射为entailment=0、contradiction=1、neutral=2。
文本清洗去除 LaTeX 公式、合并连续空格，确保文本规范化（如extract_text函数处理）。

数据处理关键步骤​

  1. 数据读取与解析read_snli函数： 过滤无效标签行，提取纯净的前提、假设、标签列表。

  2. 数据集类实现（SNLIDataset）

    • 初始化：
      • 分词：使用d2l.tokenize按单词分词。
      • 词表构建：合并前提和假设的词元，过滤低频词（min_freq=5），保留填充符<pad>，词表大小约 1.7 万。
    • 序列处理： _pad方法：截断/填充序列至固定长度（如num_steps=50），确保批量输入形状一致。
    • 访问接口：__getitem__返回元组((前提索引, 假设索引), 标签)，支持批量加载。

  3. 数据迭代器生成 load_data_snli 函数：

    • 训练集随机打乱，测试集顺序加载，使用多线程加速（num_workers）。
  • 强制测试集使用训练集词表，避免未知词元干扰模型评估。

关键问题​

问题：SNLIDataset类如何确保输入序列的一致性？​

答案：

  • 截断与填充：通过_pad方法，将所有序列长度固定为num_steps（如 50），超长截断，过短补<pad>（索引 0），确保批量输入形状统一（如(batch_size, 50)）；
  • 共享词表：测试集使用训练集构建的词表，未知词元统一处理，避免因词表差异导致的评估偏差，保证模型输入的一致性和可复现性。

自然语言推断：使用注意力​

鉴于许多模型都是基于复杂而深度的架构，Parikh 等人提出用注意力机制解决自然语言推断问题，并称之为“可分解注意力模型” 。这使得模型没有循环层或卷积层.

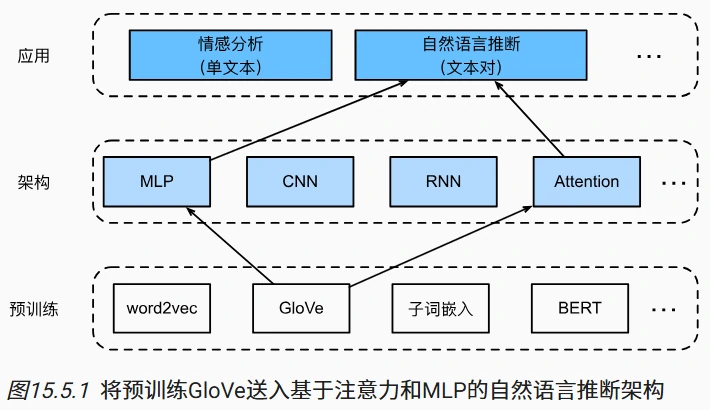
可分解注意力模型

可分解注意力模型​

  1. 对齐（Attending）
    • 目标：通过注意力机制实现前提与假设词元的软对齐
    • 方法：
      • 输入：前提词向量$A \in \mathbb{R}^{m \times d}$，假设词向量$B \in \mathbb{R}^{n \times d}$（d=100）
      • 多层感知机$f$：输出隐藏层维度 200，计算注意力分数$e_{ij} = f(a_i)^\top f(b_j)$
      • 归一化：softmax 生成权重，计算对齐向量$\beta_i = \sum_j \text{softmax}(e_{ij}) b_j$（假设对齐前提），$\alpha_j = \sum_i \text{softmax}(e_{ij}) a_i$（前提对齐假设）
    • 实现类：Attend，输出形状为$(\text{批量大小}, \text{词元数}, \text{嵌入维度})$
  2. 比较（Comparing）
    • 目标：生成词元与对齐向量的比较特征
    • 方法：
      • 连结词元与对齐向量：$[a_i, \beta_i]$、$[b_j, \alpha_j]$
      • 多层感知机$g$：输出隐藏层维度 200，生成比较向量$v_{A,i}, v_{B,j}$
    • 实现类：Compare，输出两组比较向量$V_A, V_B$
  3. 聚合（Aggregating）
    • 目标：汇总比较向量，预测逻辑关系
    • 方法：
      • 求和比较向量：$v_A = \sum_i v_{A,i}$，$v_B = \sum_j v_{B,j}$
      • 连结求和结果，通过多层感知机$h$分类，输出 3 类概率
    • 实现类：整合于模型，最终通过 softmax 生成标签

技术优势​

  1. 软对齐机制：通过注意力权重动态关联词元，捕捉“我”与“我”、“需要”与“累”等语义关联，优于固定窗口或硬对齐
  2. 分解计算：将二次复杂度（$m \times n$）降为线性（$m + n$），提升效率
  3. 端到端训练：三步骤联合优化，统一学习语义匹配与逻辑分类，避免流水线式处理误差累积

关键问题​

问题 1：可分解注意力模型为何无需循环层或卷积层即可实现高效推理？​

答案：模型通过注意力机制直接对齐词元，替代循环层的时序处理或卷积层的局部窗口，利用软对齐权重动态捕捉跨序列语义关联，将计算复杂度从序列长度的二次方降为线性，且无需递归或滑动窗口操作，因此参数更少、速度更快，适合长序列推理。

问题 2：预训练词向量（GloVe）在模型中起到什么作用？​

答案：GloVe 提供通用语义先验，如“睡眠”与“累”的相关性，减少模型在小规模数据集（SNLI）上的学习压力。通过固定嵌入层权重，避免随机初始化导致的过拟合，同时允许模型在比较和聚合步骤中聚焦于序列间关系建模，而非基础词向量学习。

问题 3：模型如何处理前提与假设长度不一致的情况？​

答案：通过填充技术（truncate_pad）将所有序列统一为固定长度（50），超长截断、过短补<pad>，确保批量输入形状一致。注意力机制天然支持不同长度序列的软对齐，权重计算仅依赖词元级交互，不要求序列等长，因此无需特殊处理长度差异。

针对序列级和词元级应用微调 BERT​

BERT 微调核心框架​

  • 最小架构更改：仅添加任务特定的全连接层，不修改 BERT 主体结构
  • 参数更新：预训练 BERT 参数全量微调，额外层参数从零初始化学习
  • 输入表示：沿用 BERT 原生格式（<cls>分类标记、<sep>分隔符）

序列级任务应用​

  1. 单文本分类 BERT单文本分类

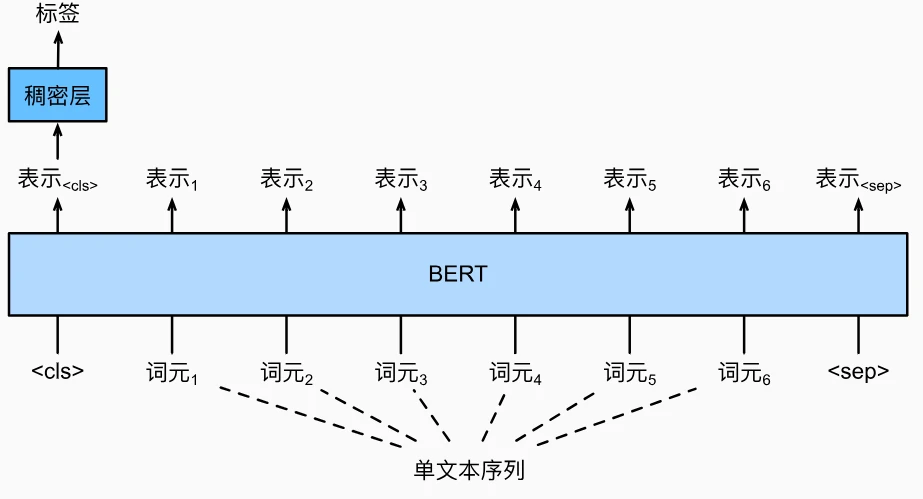
    • 输入格式：[<cls> 词元1 词元2 ... <sep>]（单文本结尾可选<sep>）
    • 核心处理：提取<cls>标记的 BERT 表示（全局语义编码），输入全连接层生成标签概率分布
    • 示例任务：
      • 情感分析（IMDb 数据集，二分类）
      • 语言可接受性判断（COLA 数据集，判断句子语法合法性）

  2. 文本对分类/回归

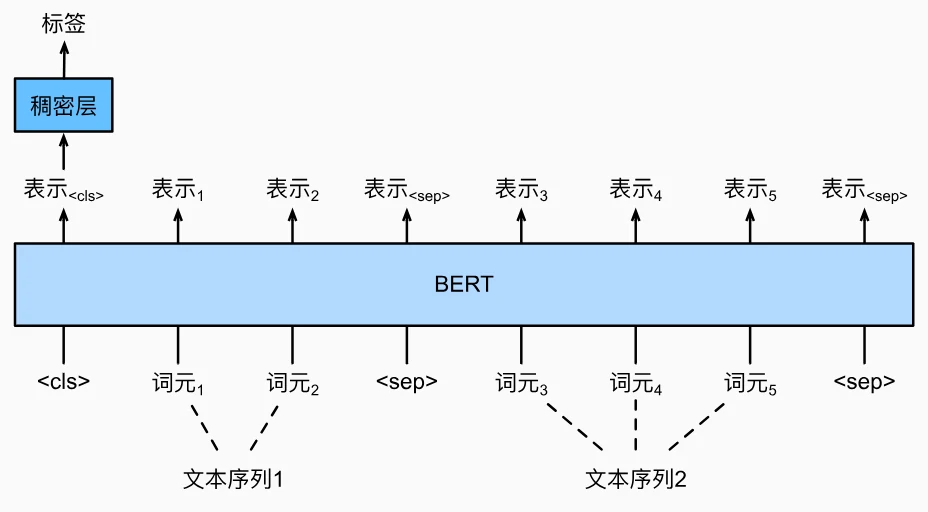
    BERT文本对分类
    • 输入格式：[<cls> 文本1词元 ... <sep> 文本2词元 ... <sep>]
    • 核心处理：
      • 分类任务：双序列拼接输入，基于<cls>表示输出离散标签（如 SNLI 的蕴涵/矛盾/中性）
      • 回归任务：输出连续相似度得分（如 STS 基准，0-5 分，均方损失）
    • 架构差异：回归任务使用均方损失，分类任务使用交叉熵损失

词元级任务应用​

  1. 文本标注（词性标注为例）

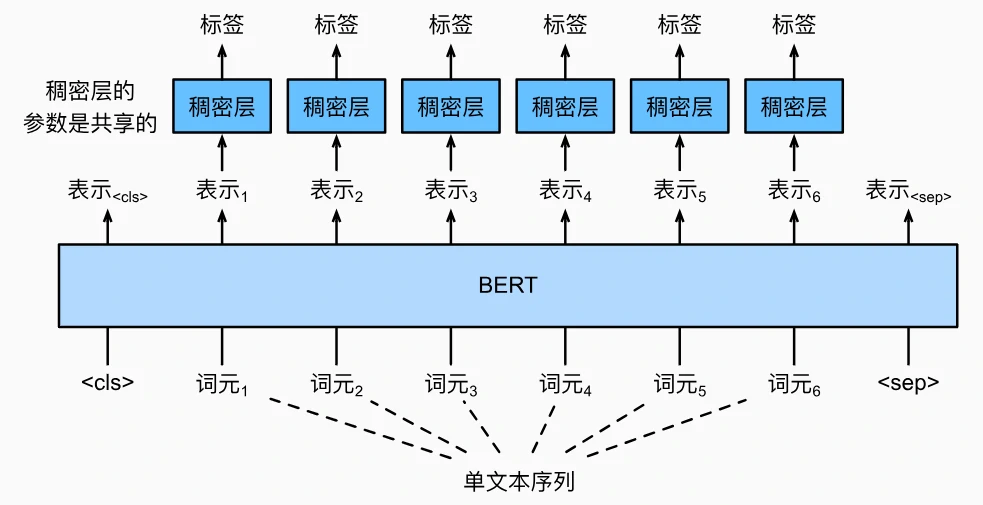
    BERT序列标注
    • 输入格式：[<cls> 词元1 词元2 ... <sep>]
    • 核心处理： 每个词元的 BERT 表示独立输入共享全连接层，输出逐词标签（如 NNP、VB、JJ 等词性标记）
    • 示例数据集：Penn 树库 II，标注句子中每个单词的词性（如“John”→NNP，“car”→NN）

  2. 问答（SQuAD v1.1）

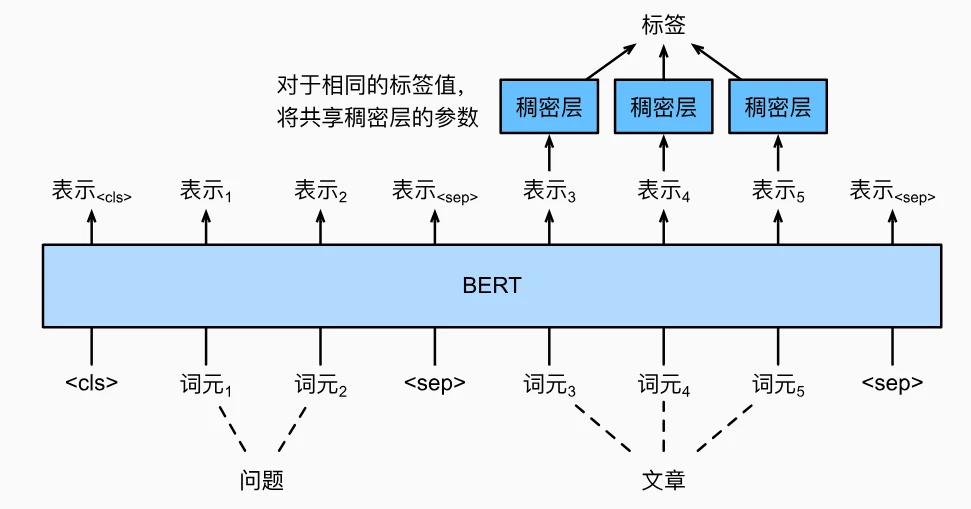
    BERT问答任务
    • 输入格式：[<cls> 问题词元 ... <sep> 段落词元 ... <sep>]
    • 核心处理：
      • 开始位置预测：词元 i 的表示 → 全连接层 → 分数 s_i，softmax 生成开始概率 p_i
      • 结束位置预测：独立全连接层 → 分数 e_j，取 i≤j 中 s_i+e_j 最大的片段作为答案
    • 训练目标：最大化真实起止位置的对数似然，支持片段级答案提取

关键任务对比表​

任务类型输入结构核心特征提取输出层配置典型数据集
单文本分类单序列+<cls><cls>全局语义向量1 层全连接（softmax）IMDb、COLA
文本对分类双序列+<cls>+<sep><cls>融合双序列信息1 层全连接（softmax）SNLI
文本标注单序列+<cls>+<sep>每个词元独立向量共享全连接层（逐词分类）Penn 树库 II
问答问题+段落+<cls>+<sep>词元级开始/结束分数2 层全连接（s_i 和 e_j 分数）SQuAD v1.1

关键问题​

问题 1：BERT 微调时为何只需添加少量额外层？​

答案：BERT 预训练阶段已学习通用语义表示（如词元级上下文、序列级语义聚合），下游任务只需通过额外全连接层将这些表示映射到特定任务输出（如分类标签、片段位置），无需修改 BERT 主体结构，实现“最少架构更改”。

问题 2：文本对分类与单文本分类的输入表示有何核心差异？​

答案：

  • 单文本分类：输入单个序列，依赖<cls>标记聚合全局语义；
  • 文本对分类：输入双序列，通过<sep>分隔，<cls>标记融合双序列交互信息，用于判断两者逻辑关系（如 SNLI 的蕴涵/矛盾）或相似度（如 STS 的连续得分）。
问题 3：问答任务中如何利用 BERT 预测答案片段？​

答案：

  • 输入为“问题+段落”双序列，通过两个独立全连接层分别生成每个词元作为答案**开始位置（s_i）和结束位置（e_j）**的分数；
  • 计算所有合法片段（i≤j）的 s_i+e_j，选择分数最高的片段作为答案，实现端到端的片段提取，无需人工设计规则。

自然语言推断：微调 BERT​

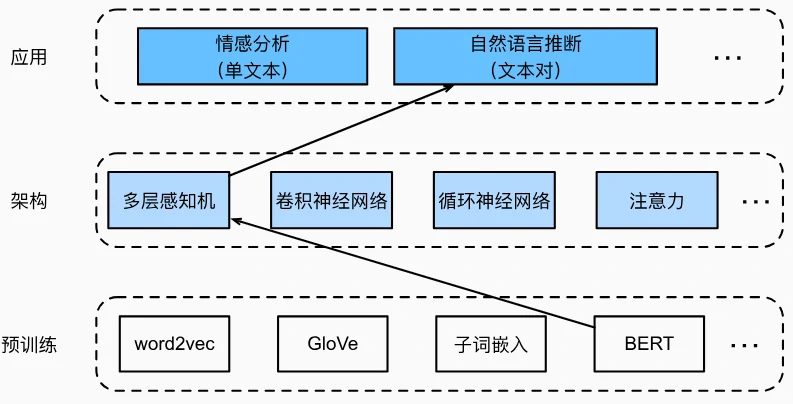
自然语言推断微调BERT

预训练 BERT 模型加载​

  • 模型版本：
    • bert.small：小版本，用于演示，包含 256 维隐藏层、4 头注意力、2 层编码器
    • bert.base：原始基础模型（练习中使用），包含 768 维隐藏层、12 头注意力、12 层编码器
  • 加载函数：load_pretrained_model
    • 下载预训练文件（包含vocab.json词表和pretrained.params参数）
    • 初始化 BERT 模型并加载参数，支持 MXNet/PyTorch/PaddlePaddle 框架
  • 设备配置：使用d2l.try_all_gpus()自动获取可用 GPU，加速训练

数据集处理：SNLIBERTDataset 类​

  • 输入处理：
    • 文本对截断：保留<CLS>、<SEP>等特殊 Token 位置，总长度超过max_len-3时，优先截断较长文本的末尾 Token
    • 填充与分段：Token ID 和段索引填充至max_len（默认 128），有效长度记录真实 Token 数
  • 并行处理：使用 4 个工作进程并行生成样本，加速数据预处理
  • 数据集加载：
    • 下载 SNLI 数据集，生成训练集（549,367 样本）和测试集（9,824 样本）
    • 使用 DataLoader 加载，批量大小 512，支持多框架数据格式

3. 微调架构：BERTClassifier​

  • 网络结构：
    • 编码器：使用预训练 BERT 的编码器，提取文本对整体语义
    • 隐藏层：复用 BERT 的隐藏层（非线性变换）
    • 输出层：单层全连接层，将<CLS>词元编码映射到 3 类（维度 3）
  • 参数更新策略：
    • 预训练的编码器和隐藏层参数微调（参与梯度更新）
    • 输出层参数从零开始学习
    • 与预训练相关的 MLM 和 NSP 任务参数不更新（标记为ignore_stale_grad）

关键问题​

问题 1：微调 BERT 时，哪些参数会被更新？​

  • 答案：仅与下游任务相关的参数会被更新，包括：

    1. BERT 编码器的所有参数（预训练后微调）
  1. 新增多层感知机的隐藏层和输出层参数（其中隐藏层参数来自预训练 BERT 的hidden层，参与微调；输出层参数从零开始学习） 预训练阶段的 MLM（遮蔽语言模型）和 NSP（下一句预测）任务相关参数不会更新，因为下游任务（自然语言推断）无需这些损失函数。
问题 2：SNLIBERTDataset 如何处理过长的文本对？​
  • 答案：采用优先截断较长文本末尾 Token 的策略：
    1. 保留 3 个特殊 Token 位置（<CLS>, <SEP>, <SEP>），允许的最大文本对长度为max_len-3
    2. 当总长度超过限制时，循环检查前提和假设的长度，每次截断较长文本的最后一个 Token
    3. 优势：简单高效，保证文本对核心信息尽可能保留；劣势：可能截断关键语义（如句尾动词），可通过按比例截断优化。