RNN神经网络
RNN循环神经网络
序列模型
股价波动、用户行为、文本语句等都是序列数据,其特点是前后数据相互关联,顺序不能打乱。序列数据的时间依赖性**使得传统机器学习模型难以处理,需专门的统计工具和神经网络架构。
统计工具:自回归与隐变量模型
AR自回归模型Autoregressive Models
- 思路:用最近的 τ 个历史数据预测当前值,如用前 4 天股价预测第 5 天股价。
- 公式:$( x_t \sim P(x_t \mid x_{t-1}, \dots, x_{t-\tau}) )$
- 优点:参数固定,可训练深度网络;缺点:仅依赖近期数据,可能忽略长距离依赖。
隐变量自回归模型Latent Autoregressive Models
- 思路:引入“隐状态”(如“市场情绪”)总结历史信息,用隐状态更新预测。
- 公式:
- 预测:$( \hat{x}_t = P(x_t \mid h_t) )$
- 隐状态更新:$( h_t = g(h_{t-1}, x_{t-1}) )$
- 优点:能捕捉更复杂的时间依赖;缺点:隐状态不可观测,需假设其动态变化。
- 公式:
马尔可夫模型(Markov Models)
- 简化假设:当前状态仅依赖前一状态(一阶马尔可夫性),如$( P(x_t \mid x_{t-1}, \dots, x_1) = P(x_t \mid x_{t-1}) )$。
- 应用场景:离散数据(如文本分词),可通过动态规划高效计算概率。
因果关系
预测分析:单步与多步预测的差异
- 内插 vs 外推:内插(已知范围内估计)较简单,外推(超出范围预测)需考虑时间动态变化,难度大。
- 模型选择:自回归模型适用于短期依赖,隐变量模型(如后续章节的 RNN)更适合捕捉长期依赖。
单步预测One-Step Prediction
- 定义:用历史数据预测下一时刻的值(k=1)。
- 效果:模型在训练数据外的预测仍较准确,因每步依赖真实历史数据,误差未累积。
多步预测Multi-Step Prediction
- 定义:用历史数据和之前的预测值递归预测未来多步(如 k=64)。
- 问题:
- 误差累积:每步预测误差会传递到下一步,导致长距离预测严重偏离(如 64 步预测趋近于常数)。
- 示例:天气预报中,24 小时内较准,超过则精度骤降。
文本预处理
文本预处理的必要性
- 计算机的“语言障碍”:
计算机只能处理数字,而文本是字符串形式(如英文单词、汉字),需要先“翻译”成数字索引。
- 例如:“机器”→ 1,“学习”→ 2,这样模型才能理解和计算。
- 核心目标:将文本转换为有序的数字序列,同时保留语义信息,减少噪声和冗余。
预处理步骤详解
1. 读取数据集
从文件中读取文本内容,存储为字符串列表。 示例:加载《时间机器》小说文本,共 3221 行。预处理:用正则表达式去除非字母字符(如标点符号),统一转换为小写字母。
-
代码演示:
def read_time_machine():
with open('timemachine.txt', 'r') as f:
lines = f.readlines()
# 去除非字母字符,转小写,去首尾空格
return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]
2. 词元化Tokenization
-
定义:将文本拆分成最小语义单元(词元),可以是单词或字符。
- 单词级词元化:按空格拆分,如“the time machine”→ ['the', 'time', 'machine']。
- 字符级词元化:拆分成单个字符,如“abc”→ ['a', 'b', 'c']。
-
代码演示:
def tokenize(lines, token='word'):
if token == 'word':
return [line.split() for line in lines] # 按单词拆分
elif token == 'char':
return [list(line) for line in lines] # 按字符拆分
tokens = tokenize(lines) # 得到词元列表的列表
3. 构建词表Vocabulary
-
作用:将词元映射到唯一的数字索引,便于模型输入。
-
步骤:
- 统计词频:计算每个词元在语料中出现的频率。
- 过滤低频词:丢弃出现次数少于阈值(如 min_freq=1)的词元,减少词表大小。
- 分配索引:
- 保留特殊词元:未知词元(,索引 0)、填充词元()等。
- 按词频排序,高频词优先获得低索引(如“the”→ 1,“machine”→ 2)。
-
代码演示:
class Vocab:
def __init__(self, tokens, min_freq=0, reserved_tokens=None):
counter = collections.Counter(tokens) # 统计词频
# 按频率从高到低排序,保留高频词
self.idx_to_token = ['<unk>'] + (reserved_tokens or [])
self.token_to_idx = {token: idx for idx, token in enumerate(self.idx_to_token)}
for token, freq in sorted(counter.items(), key=lambda x: -x[1]):
if freq >= min_freq and token not in self.token_to_idx:
self.idx_to_token.append(token)
self.token_to_idx[token] = len(self.idx_to_token) - 1 -
示例:词表中的映射关系: '' → 0,'the' → 1,'time' → 2,'machine' → 3,...
完整流程示例
-
输入原始文本:
"The Time Machine by H.G. Wells" -
读取并清洗:转换为小写,去除标点 → "the time machine by h g wells"。
-
词元化(单词级):拆分为 ['the', 'time', 'machine', 'by', 'h', 'g', 'wells']。
-
构建词表:词表包含这些词元,映射为索引序列 [1, 2, 3, 4, 5, 6, 7]。
-
未知词处理:若出现未登录词(如'hello'),统一映射为 0()。
语言模型和数据集
语言模型
- 简单理解:语言模型是一种计算文本序列概率的模型,用来判断一段文字是否“像人话”。
- 例如:判断“我吃饭”和“饭吃我”哪个更合理,前者概率更高。
语言模型的作用
- 消除歧义:
- 语音识别中,“to recognize speech”和“to wreck a nice beach”发音相似,语言模型可根据语义选择正确的文本。
- 断句问题:“我想吃奶奶” vs “我想吃,奶奶”,后者更符合常理。
- 生成自然文本:
- 基于前文生成合理的后续内容,如聊天机器人、自动写作等。
- 虽然目前模型还不能真正“理解”文本,但能生成语法正确的内容。
训练语言模型
1. 统计方法:从数据中学习概率
- 基本思路:
通过统计语料库中单词和单词组合的频率来估计概率。
- 单词语概率:$( P(\text{deep}) = \frac{\text{“deep”出现次数}}{\text{总单词数}} )$。
- 条件概率(如二元语法):$( P(\text{learning}|\text{deep}) = \frac{\text{“deep learning”出现次数}}{\text{“deep”出现次数}} )$。
- 问题与挑战:
- 低频词问题:罕见单词或组合(如“deep learning is fun”)出现次数少,统计不准确。
- 存储问题:需记录所有单词组合的频率,数据量大时内存不足。
- 语义缺失:无法捕捉单词间的语义关联(如“猫”和“猫科动物”)。
- 解决方案:拉普拉斯平滑 给低频词的计数添加一个小常数,避免零概率问题。例如:$P(\text{x}) = \frac{n(\text{x}) + \epsilon}{n + m\epsilon} \quad (\epsilon \text{是平滑参数,} m \text{是单词种类数})$
2. 马尔可夫模型与 n 元语法
- 马尔可夫假设:
假设当前词只依赖前 k 个词(k 阶马尔可夫链),简化计算。
- 一元语法(unigram):独立假设,$( P(x_1, x_2) = P(x_1)P(x_2) )$(不考虑上下文)。
- 二元语法(bigram):依赖前一个词,$( P(x_2|x_1) )$(如“吃饭”中“饭”依赖“吃”)。
- 优缺点:
- 优点:计算复杂度随 k 增长可控(k=3 时只需记录三个词的组合)。
- 缺点:k 较大时仍需大量数据,且无法捕捉长距离依赖(如段落级上下文)。
RNN循环神经网络
传统神经网络的局限无法捕捉序列数据中的时间依赖关系(如前后单词的顺序影响),为此诞生了RNN,通过隐状态捕捉上下文。
循环神经网络(RNN)的核心创新:隐状态(记忆机制)
Recurrent Neural Network
- 隐状态的作用:
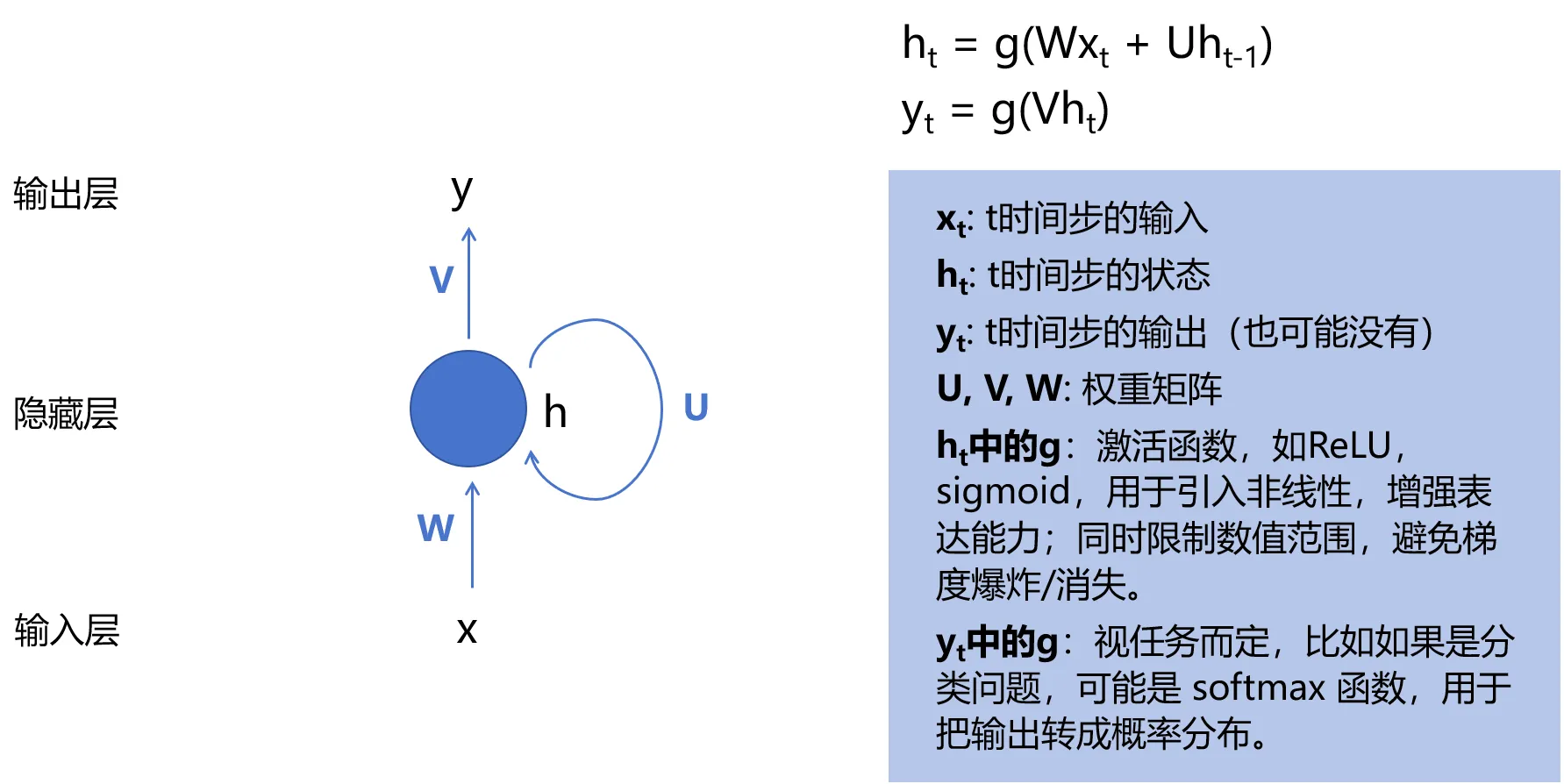
RNN 引入“隐状态”(记作$( h_t )$)来存储过去序列的信息,允许当前时间步的计算依赖于前序步骤的结果。
- 例如:预测“我吃饭”的下一个词时,$( h_t )$会记录“我”和“吃”的信息,帮助判断下一个词更可能是“饭”而非“书”。
- 计算逻辑:
- 当前时间步的隐状态$( h_t )$由两部分决定:
- 当前输入$( X_t )$(如当前词的特征);
- 前一时间步的隐状态$( h_{t-1} )$(如之前词的上下文信息)。
- 公式:$( h_t = \phi(X_t W_{xh} + h_{t-1} W_{hh} + b_h) )$,其中$( \phi )$是激活函数(如 ReLU),$( W_{xh} )$和$( W_{hh} )$是权重矩阵,用于融合输入和历史信息。
- 当前时间步的隐状态$( h_t )$由两部分决定:
- 参数共享机制:
不同时间步共享同一组权重参数($( W_{xh}, W_{hh} )$等),避免了参数随时间步增长的问题,大幅降低计算复杂度。
RNN 的结构与计算流程
- 展开的时间维度:
RNN 在时间轴上展开后,每一步的计算逻辑相同,但隐状态会逐步积累序列信息。
- 例如:处理“machine”序列时,每个字符(m, a, c, h, i, n)依次输入,隐状态$( h_t )$逐渐包含整个前缀的信息,用于预测下一个字符(如“m”→“a”,“ma”→“c”等)。
- 输入与输出:
- 输入:每个时间步的词元(如字符)通过嵌入层转换为向量($( X_t )$)。
- 输出:通过全连接层将隐状态映射为词表上的概率分布(如预测下一个字符的概率)。
- 示例:输入序列“machin”,标签序列为“achine”,模型通过学习每个位置的条件概率(如 P('a'|'m'), P('c'|'ma'), 等)生成下一个字符。
字符级语言模型:用 RNN 生成文本
- 任务定义:
根据前序字符预测下一个字符,属于序列生成问题。
- 例如:输入“hel”,模型输出“lo”的概率较高,生成“hello”。
- 训练方法:
- 数据预处理:将文本拆分为字符序列,移位后作为输入-标签对(如输入“abcd”,标签“bcde”)。
- 损失函数:交叉熵损失,衡量预测概率与真实标签的差异。
- 优化目标:最小化困惑度(Perplexity),其定义为平均交叉熵损失的指数,值越小表示模型预测越准确。
- 完美模型的困惑度为 1,随机猜测模型的困惑度等于词表大小。
困惑度(Perplexity):评估语言模型的指标
- 直观理解:
衡量模型预测下一个词元的“不确定性”,等价于“平均可选词元数”。
- 示例:
- 困惑度=1:模型完全确定下一个词元(如 P(‘a’|‘h’) = 1)。
- 困惑度=1000:模型预测等价于从 1000 个词元中随机选择。
- 示例:
- 作用:
用于比较不同模型的性能,例如:
- RNN 的困惑度低于 n 元语法模型,说明其捕捉依赖关系的能力更强。
- 字符级模型的困惑度通常高于单词级模型,因字符的语义信息更少。
RNN 的优势与局限
- 优势: 能捕捉序列中的时间依赖,适合处理文本、语音等时序数据。 参数共享机制使其适用于长序列,避免维度灾难。
- 局限:
- 长期依赖问题:隐状态随时间传递时可能丢失早期信息。
- 计算效率:每个时间步需等待前一步完成,难以并行处理。
循环神经网络的从零开始实现
准备工作:数据预处理与编码
- 数据加载与清洗: 以《时间机器》文本为例,加载数据后去除标点符号并转为小写,拆分为字符序列。例如,原文“Hello!”→“hello”。
- 独热编码(One-Hot Encoding):
将每个字符转换为唯一的二进制向量(如字符“a”→[1,0,0,...],“b”→[0,1,0,...]),便于神经网络处理。
- 缺点:词表大时向量维度高(如 26 个字母需 26 维),且无法捕捉字符间语义关联。
模型构建:从参数初始化到前向传播
- 参数初始化: 定义隐藏层和输出层的权重矩阵($W_{xh}, W_{hh}, W_{hq}$)和偏置($b_h, b_q$),随机初始化并附加梯度以便训练。
- 隐状态初始化: 初始隐状态为全零张量,形状为(批量大小,隐藏单元数),用于存储序列的历史信息。
- 前向传播逻辑:
- 对每个时间步的输入(独热向量),结合前一隐状态计算当前隐状态: $$h_t = \tanh(X_t W_{xh} + h_{t-1} W_{hh} + b_h)$$
- 通过输出层将隐状态转换为字符概率分布: $$o_t = h_t W_{hq} + b_q$$
- 示例:输入“time”,逐个字符计算隐状态,最终输出“t”“i”“m”“e”的预测概率。
模型训练:从预测到梯度优化
- 预测函数(预热与生成):
- 预热期:输入前缀字符(如“time”),更新隐状态但不输出,使模型“理解”上下文。
- 生成期:基于预热后的隐状态,逐字符预测后续内容(如生成“traveller”)。
- 梯度裁剪(Gradient Clipping):
- 原因:长序列反向传播时梯度可能爆炸(数值不稳定)。
- 方法:将梯度范数限制在阈值内(如 θ=1),避免参数更新过大导致模型发散。
- 训练循环:
- 随机采样或顺序划分数据,前者每次随机截断序列(需重新初始化隐状态),后者保留相邻序列的隐状态连续性。
- 使用交叉熵损失衡量预测与真实字符的差异,通过随机梯度下降(SGD)优化参数。
- 评估指标:困惑度(Perplexity),值越小表示预测越准确(完美模型为 1)。
通过时间反向传播
什么是通过时间反向传播(BPTT)
- 本质:它是反向传播算法在循环神经网络(RNN)中的应用,用于计算模型参数的梯度。
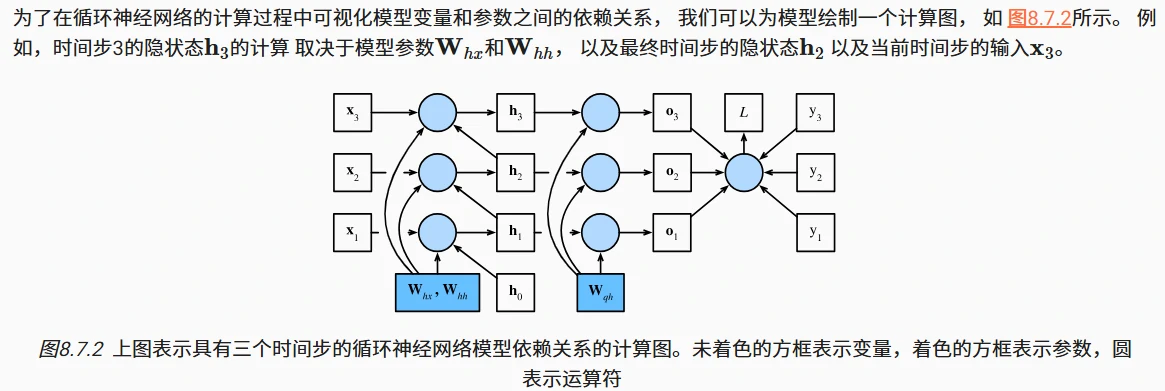
- 原理:将 RNN 按时间步展开成一个链式结构(类似多层神经网络),然后从最后一个时间步开始,反向计算每个参数的梯度。
- 目标:通过链式法则,计算损失函数对所有参数(如隐藏层权重$W_{hx}$、$W_{hh}$,输出层权重$W_{qh}$)的梯度,以便进行参数更新。
RNN 的梯度计算难题:梯度消失/爆炸
- 问题根源:RNN 的隐状态$h_t$依赖于前一个时间步的隐状态$h_{t-1}$,导致梯度计算时出现 矩阵的高次幂(如$W_{hh}^{\top}$的幂次)。
- 若矩阵特征值 小于 1,梯度会随时间步长指数级衰减(梯度消失);
- 若特征值 大于 1,梯度会指数级增长(梯度爆炸)。
- 影响:长序列(如 1000 个时间步)的梯度计算在计算上不可行(耗时耗内存),且数值不稳定,导致模型难以训练。
解决方案:截断反向传播
为解决长序列梯度计算的难题,常见方法是截断时间步长,仅计算最近若干步的梯度:
- 常规截断(固定长度截断)
- 将序列分割为固定长度的子序列(如每 50 步一段),对每个子序列独立进行反向传播。
- 优点:计算量大幅减少,数值稳定性提高;
- 缺点:忽略长距离依赖,模型更关注短期信息。
- 随机截断
- 随机决定截断的时间步长(用概率$π_t$控制是否终止反向传播),长序列出现概率低但权重更高。
- 理论优势:可能捕获部分长距离依赖;
- 实际问题:方差较大,效果不一定优于常规截断。
- 完全计算(仅理论探讨)
- 直接计算所有时间步的梯度,但仅适用于极短序列,实际中不可行(计算量爆炸)。
 ## 改进的循环神经网络
## 改进的循环神经网络
门控循环单元 GRU
门控循环单元(GRU)——一种改进的循环神经网络(RNN),旨在解决传统 RNN 中梯度消失、长期依赖等问题。
为什么需要 GRU
传统 RNN 在处理长序列时存在两个大问题:
- 梯度消失/爆炸:远距离的前后数据关联难以捕捉(比如“我早上吃了饭,所以现在不饿”中,“早上”和“现在”的关联)。
- 无法选择性记忆:对所有数据同等处理,无法忽略无关信息(如文本中的噪声符号)或重置状态(如章节切换时)。
GRU 通过引入门控机制解决这些问题,让模型能自动选择记忆或遗忘哪些信息。
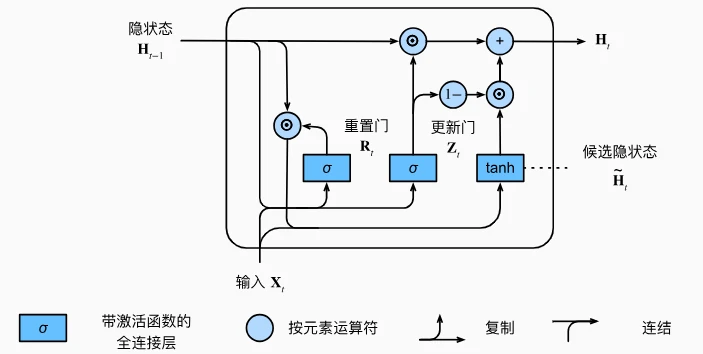
GRU 的核心:两个“门”
GRU 有两个关键门控,均为 0 到 1 之间的向量(通过神经网络学习得到):
- 重置门(Reset Gate)
- 作用:控制“忘记多少过去的隐状态”。
- 通俗理解:
- 当重置门接近 1 时,保留过去的隐状态,类似传统 RNN。
- 当重置门接近 0 时,忽略过去的隐状态,只关注当前输入(比如遇到新章节时,重置状态)。
- 应用场景:捕捉短期依赖(如一句话中的前后词关联)。
- 更新门(Update Gate)
- 作用:控制“保留多少旧隐状态”和“引入多少新候选隐状态”。
- 通俗理解:
- 当更新门接近 1 时,几乎保留全部旧隐状态,忽略当前输入(比如长期记忆的重要信息,如“出生年份”对后续年龄计算的影响)。
- 当更新门接近 0 时,用新候选隐状态完全替换旧状态(比如处理新的无关内容时,清空旧记忆)。
- 应用场景:捕捉长期依赖(如跨段落的主题关联)。
GRU 的工作流程
- 计算门控: 输入当前数据和前一时刻的隐状态,通过神经网络生成重置门(R)和更新门(Z)。
- 生成候选隐状态: 根据重置门决定是否“擦除”旧隐状态,再结合当前输入生成新的候选隐状态(类似传统 RNN 的隐状态更新,但受重置门控制)。
- 更新隐状态: 通过更新门对旧隐状态和候选隐状态进行“混合”,得到最终的新隐状态。
- 公式直观理解:
新隐状态 = 旧隐状态 * 更新门 + 候选隐状态 * (1 - 更新门)(相当于在旧状态和新状态之间选一个“比例”)
- 公式直观理解:
长短期记忆网络 LSTM
长短期记忆网络(LSTM)——一种经典的循环神经网络(RNN)变体,专门用于解决传统 RNN 在处理长序列时的梯度消失和长期依赖问题。
为什么需要 LSTM
传统 RNN 的隐状态更新机制会导致:
- 远距离信息丢失:比如“我 5 岁学会游泳,现在 30 岁仍擅长”中,“5 岁”和“30 岁”的关联难以捕捉。
- 无法选择性遗忘:对所有信息一视同仁,无法主动丢弃噪声(如文本中的无关符号)。
LSTM 通过引入记忆元(Memory Cell)和三个门控机制,让模型能像人类一样选择性记忆、遗忘或输出信息。
LSTM 的核心:三个“门”和记忆元
1. 记忆元(Cell)
- 作用:相当于“存储仓库”,专门记录长期信息(如“5 岁学会游泳”)。
- 特点:通过门控机制控制数据的写入和读取,避免梯度消失。
2. 三个门控
每个门都是 0 到 1 之间的向量(通过神经网络学习得到),用于控制信息的流动:
(1)遗忘门(Forget Gate)
- 作用:决定“丢弃多少记忆元中的旧信息”。
- 接近 1:保留旧信息(如长期有效的知识);
- 接近 0:丢弃旧信息(如过时的临时数据)。
- 例子:读文章时,遇到新章节,遗忘门会丢弃前一章节的无关细节。
(2)输入门(Input Gate)
- 作用:决定“允许多少新信息写入记忆元”。
- 接近 1:接受新信息(如当前句子的关键词);
- 接近 0:拒绝新信息(如噪声符号)。
- 例子:翻译句子时,输入门只允许有用词汇进入记忆元。
(3)输出门(Output Gate)
- 作用:决定“输出多少记忆元中的信息到隐状态”。
- 接近 1:输出信息用于预测(如生成下一个词);
- 接近 0:保留信息不输出(如暂时用不到的背景知识)。
- 例子:生成文本时,输出门根据当前需求决定是否使用记忆元中的历史信息。
LSTM 的工作流程
- 计算三个门:
- 输入当前数据和前一时刻的隐状态,生成遗忘门(F)、输入门(I)、输出门(O)。
- 生成候选记忆元:
- 根据当前输入和隐状态,生成待写入记忆元的新候选值(类似草稿)。
- 更新记忆元:
- 遗忘阶段:用遗忘门过滤旧记忆元中的信息(
旧记忆 * 遗忘门)。 - 输入阶段:用输入门选择候选记忆元中的新信息(
候选记忆 * 输入门)。 - 合并:旧记忆的保留部分 + 新信息的接受部分 = 新记忆元。
- 遗忘阶段:用遗忘门过滤旧记忆元中的信息(
- 计算隐状态:
- 用输出门控制记忆元的输出:
隐状态 = 输出门 * tanh(新记忆元)。 (tanh 确保值在-1 到 1 之间,输出门决定漏出多少信息)
- 用输出门控制记忆元的输出:
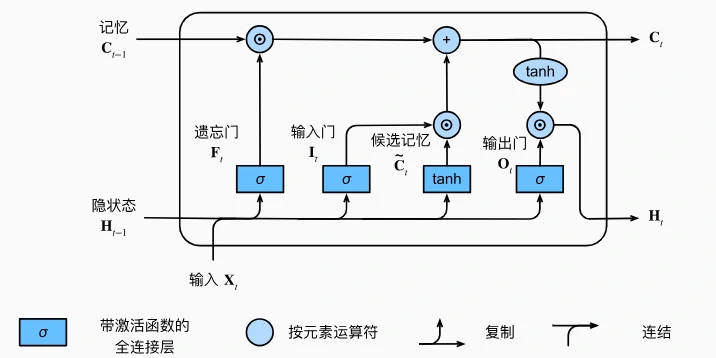
LSTM 与 GRU 的对比
- 门控数量:LSTM 有 3 个门,GRU 有 2 个门(合并了输入门和遗忘门为更新门)。
- 复杂度:LSTM 计算更复杂,但灵活性更高;GRU 更简单,训练速度更快。
- 效果:两者均能解决长期依赖问题,实际应用中根据任务选择(如复杂场景用 LSTM,轻量场景用 GRU)。
深度循环神经网络
深度循环神经网络(深度 RNN),即通过堆叠多个循环层(如 LSTM、GRU 等)来增强模型对复杂序列的建模能力。
为什么需要深度 RNN
- 单层 RNN 的局限:单层 RNN(如简单 RNN、GRU、LSTM)虽然能处理序列数据,但对复杂任务(如长文本语义理解、多尺度时间模式分析)的建模能力有限。
- 例如:分析金融数据时,需要同时捕捉短期波动(分钟级)和长期趋势(季度级),单层网络难以兼顾。
- 深度 RNN 的优势:通过堆叠多层循环层,每一层专注于不同层次的特征,实现“分层抽象”:
- 底层:捕捉局部、短期特征(如文本中的单词搭配)。
- 高层:捕捉全局、长期特征(如文本的主题或情感)。
深度 RNN 的结构与原理
1. 网络架构
- 多层循环层堆叠:每层循环层的隐状态同时传递给下一时间步和下一层循环层
- 例如:第 1 层处理原始输入(如单词向量),第 2 层基于第 1 层的输出进一步提取高层特征。
- 数学表达:第$l$层的隐状态$H_t^{(l)}$由以下公式计算:$$H_t^{(l)} = \phi_l\left( H_t^{(l-1)} W_{xh}^{(l)} + H_{t-1}^{(l)} W_{hh}^{(l)} + b_h^{(l)} \right)$$
- $H_t^{(l-1)}$:当前层的输入(来自上一层的隐状态)。
- $H_{t-1}^{(l)}$:当前层前一时间步的隐状态(循环连接)。
- $\phi_l$:激活函数(如 tanh、sigmoid)。
2. 与单层 RNN 的区别
- 信息流动方向: 除了时间维度的循环连接(横向),还增加了层间的垂直连接,形成“多层流水线”。
- 参数规模: 每层都有独立的权重矩阵(如$W_{xh}^{(l)}$、$W_{hh}^{(l)}$),参数总量随层数增加而显著增长。
实现深度 RNN
1. 框架内置支持
主流深度学习框架(如 PyTorch、TensorFlow)提供了多层循环层的简洁接口,只需指定层数和隐藏单元数:
# 以PyTorch为例,定义两层LSTM
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers=2) # num_layers=2表示两层
2. 训练注意事项
- 计算成本高: 多层循环层会显著增加训练时间和显存占用(例如,两层 LSTM 的计算量约为单层的 2 倍)。
- 梯度消失/爆炸风险: 虽然 LSTM/GRU 缓解了单层的梯度问题,但深层网络仍可能因层间传递导致梯度不稳定,需谨慎初始化参数和选择优化器。
- 超参数调整:
- 层数(num_layers):通常 2-4 层,过多易过拟合。
- 隐藏单元数(num_hiddens):需与层数匹配,避免底层信息不足。
双向循环神经网络
双向循环神经网络(Bi-RNN),核心是解决传统单向 RNN 无法利用未来信息的问题。通过同时运行前向和后向两个 RNN,让模型在每个时间步都能同时获取过去和未来的上下文信息,提升预测准确性。
隐马尔科夫模型的动态规划
双向 RNN 的核心原理
1. 结构设计
- 前向 RNN:从序列起点(左)向右处理数据,捕捉过去信息(如“我”“饿了”)。
- 后向 RNN:从序列终点(右)向左处理数据,捕捉未来信息(如“吃半头猪”)。
- 输出合并:每个时间步的隐状态由前向和后向的隐状态拼接或加权求和得到,输入到输出层进行预测。
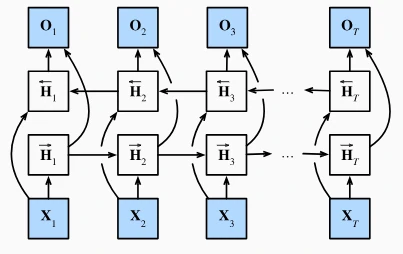
2. 数学直观
假设序列为$x_1, x_2, \dots, x_T$:
- 前向隐状态$\vec{h}_t$:依赖$x_1$到$x_t$的信息。
- 后向隐状态$\overleftarrow{h}_t$:依赖$x_T$到$x_t$的信息。
- 最终隐状态$h_t = [\vec{h}_t; \overleftarrow{h}_t]$(拼接),包含双向信息。
3. 与隐马尔可夫模型(HMM)的关联
网页通过 HMM 的动态规划原理说明:
- 传统单向 RNN 类似 HMM 的前向递归(从左到右计算概率)。
- 双向 RNN 则补充了后向递归(从右到左),类似 HMM 中同时利用前向和后向信息优化预测,避免单一方向的信息缺失。
典型应用场景
- 自然语言处理:
- 文本填空、命名实体识别(如区分“Green”是人名还是颜色,需前后文语境)。
- 机器翻译(目标语言生成需同时考虑源语言的前后文)。
- 语音识别:语音信号的上下文依赖(如“xian”可能是“先”或“线”,需前后音素判断)。
- 时间序列预测:若未来数据可获取(如已知部分未来值),双向 RNN 可提升预测精度。
注意事项
-
数据要求: 双向 RNN 需要完整的序列数据(未来信息已知),不适用于实时流式数据(如逐字生成文本时,未来词未知)。
-
框架支持:
主流框架(如 PyTorch、TensorFlow)提供双向 RNN 接口,只需设置 bidirectional=True
# PyTorch示例:双向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers=1, bidirectional=True)
机器翻译与数据集
掌握基本的实践过程
什么是机器翻译
- 定义:将文本从一种语言(源语言,如英语)自动翻译成另一种语言(目标语言,如法语)的过程。
- 历史与方法:
- 早期以统计方法为主(如统计机器翻译,需人工设计规则和模型)。
- 现代主流是神经机器翻译(NMT),基于神经网络端到端学习,无需人工拆解任务。
- 关键挑战: 源语言和目标语言的序列长度、语法结构不同,需模型捕捉跨语言的语义对应关系。
为什么预处理如此重要
- 模型输入要求:神经网络只能处理数值化的批量数据,预处理将自然语言转换为模型可理解的格式。
- 效率与性能:统一序列长度可加速矩阵运算(如 GPU 并行计算),有效长度避免无效计算(如忽略填充词元的梯度)。
- 后续模型基础:预处理后的数据集是训练编码器-解码器架构(如 Transformer)的基石,直接影响翻译质量。
编码器-解码器架构
编码器-解码器(Encoder-Decoder)架构是处理序列转换问题(如机器翻译)的核心框架。
- 处理变长序列:传统神经网络难以直接处理长度变化的输入输出,编码器-解码器通过“压缩-解压”解决此问题。
- 模块化设计:编码器和解码器可独立设计(如编码器用双向 RNN,解码器用单向 RNN),灵活适配不同任务。
编码器-解码器架构
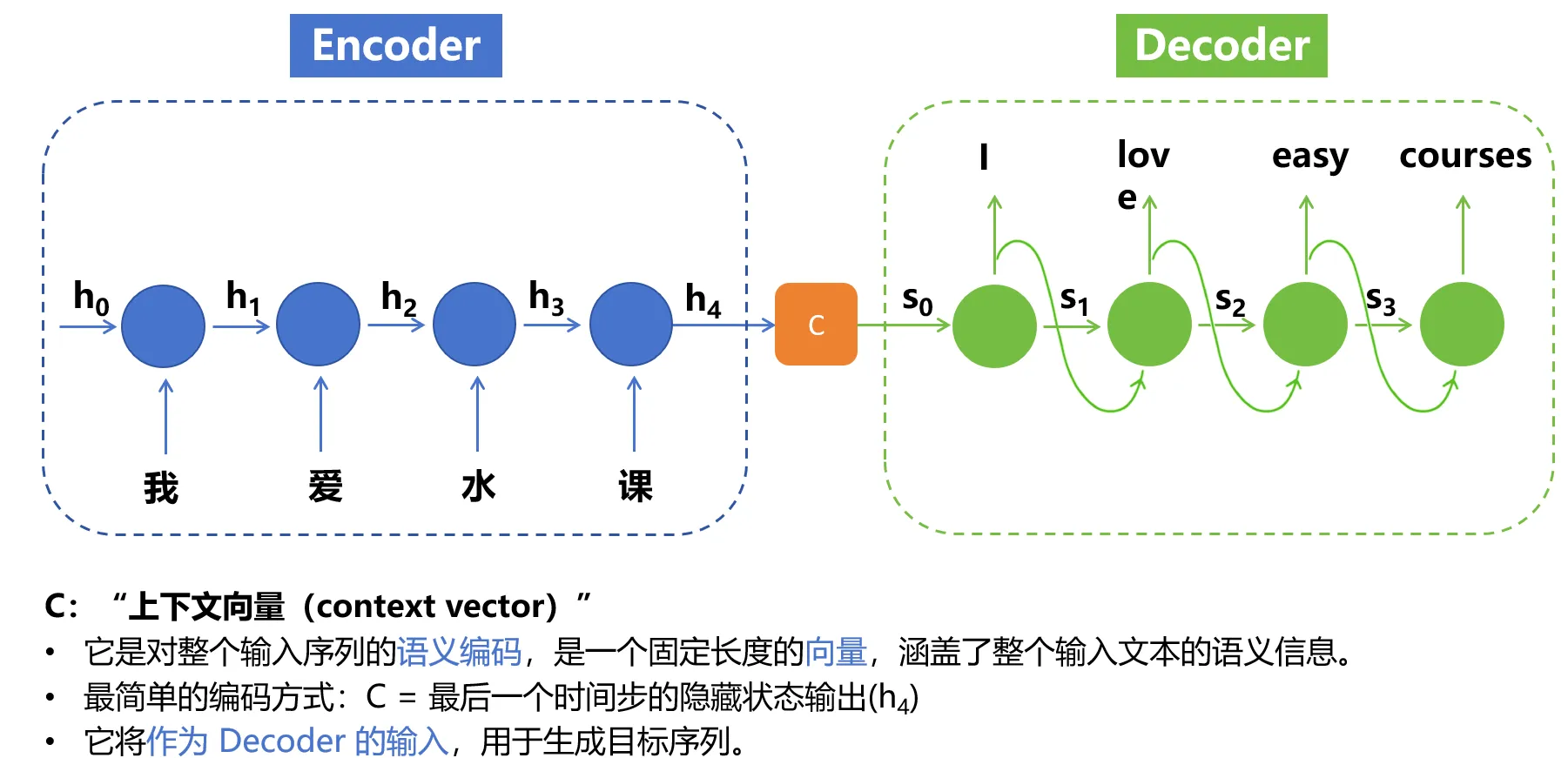
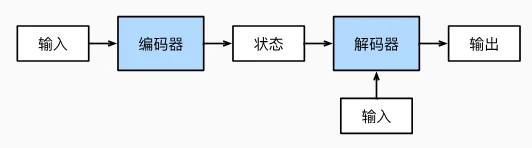
- 核心思想:将一个长度可变的序列(如英文句子)转换为另一个长度可变的序列(如法语翻译),分为两个阶段:
- 编码器(Encoder):把输入序列“压缩”成一个固定形状的编码状态(类似语义向量)。
- 解码器(Decoder):根据编码状态“解压”生成目标序列(如逐个词生成翻译)。
- 类比场景: 输入:“They are watching.” → 编码器压缩成“他们正在观看”的语义向量 → 解码器生成法语“Ils regardent.”。
编码器:压缩输入序列
-
功能:接收任意长度的输入序列(如单词列表),输出固定长度的编码状态(如向量)。
-
关键特性:
- 隐藏具体实现细节,只需满足“输入序列 → 编码状态”的接口。
- 可使用循环神经网络(RNN)、Transformer 等实现。
-
代码接口(以 PyTorch 为例):
class Encoder(nn.Module):
def __init__(self):
super().__init__()
def forward(self, X): # X是输入序列(如词元ID数组)
raise NotImplementedError # 具体实现由子类完成
解码器:生成目标序列
-
功能:根据编码器的编码状态,逐个生成目标序列的词元(如翻译后的单词)。
-
关键步骤:
- 初始化状态:用编码器输出的编码状态生成解码器的初始状态。
- 逐词生成:每次输入一个词元(如起始符
<bos>)和当前状态,输出下一个词元及更新后的状态,直到生成结束符<eos>。
-
代码接口(以 PyTorch 为例):
class Decoder(nn.Module):
def __init__(self):
super().__init__()
def init_state(self, enc_outputs): # 用编码器输出初始化状态
raise NotImplementedError
def forward(self, X, state): # X是当前输入词元,state是当前状态
raise NotImplementedError # 返回生成的词元及新状态
合并编码器和解码器
-
整体流程:
- 编码器处理输入序列,得到编码状态。
- 解码器用编码状态初始化,逐个生成目标序列词元。
-
代码框架(以 PyTorch 为例):
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder):
super().__init__()
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X): # enc_X是输入序列,dec_X是目标序列(训练时用)
enc_outputs = self.encoder(enc_X) # 编码
dec_state = self.decoder.init_state(enc_outputs) # 初始化解码器状态
return self.decoder(dec_X, dec_state) # 解码生成目标序列- 训练时:dec_X 是目标序列的输入(含
<bos>等符号)。 - 推理时:dec_X 可逐词生成(如先输入
<bos>,再根据输出逐步添加新词元)。
- 训练时:dec_X 是目标序列的输入(含
序列到序列学习
序列到序列(Seq2Seq)模型是编码器-解码器架构的具体实现,用于解决机器翻译等序列转换问题。
Seq2Seq 模型的核心架构
Seq2Seq 模型由**编码器(Encoder)和解码器(Decoder)两部分组成:
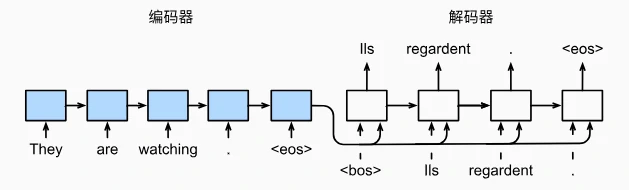
- 编码器:
- 功能:将输入序列(如英文句子)转换为一个固定长度的上下文向量(Context Vector),浓缩输入序列的语义信息。
- 实现:
- 输入序列先通过嵌入层(Embedding Layer)转换为词向量。
- 词向量输入到多层 RNN(如 GRU)中,最终输出所有时间步的隐状态,通常取最后一个时间步的隐状态作为上下文向量。
- 示例:输入“They are watching.”,编码器输出一个包含语义的向量(如“他们正在观看”的抽象表示)。
- 解码器:
- 功能:根据编码器的上下文向量,逐个生成目标序列(如法语翻译)的词元。
- 实现:
- 初始化时,用编码器的最后一个隐状态作为解码器的初始隐状态。
- 输入序列的开始符号(
<bos>)和上下文向量,通过多层 RNN 逐词生成目标序列,直到遇到结束符号(<eos>)。
- 示例:根据上下文向量,解码器逐步生成“Ils”“regardent”“.”“”。
关键技术细节
1. 输入输出处理
- 嵌入层:将词元(如单词)转换为连续的特征向量,捕捉词间语义关系(如“run”和“cours”在向量空间中接近)。
- 序列填充与掩码:
- 对不同长度的序列进行填充(如添加
<pad>)使其等长,便于批量训练。 - 使用**掩码(Mask)**忽略填充词元的损失计算,避免无效数据干扰训练。
- 对不同长度的序列进行填充(如添加
2. 上下文向量的传递
- 编码器的最后一个隐状态作为解码器的初始隐状态,将输入序列的全局信息传递给解码器。
- 解码器在每个时间步将当前词向量与上下文向量拼接,指导目标词元的生成。
3. 损失函数与训练
- 损失计算:使用交叉熵损失函数,仅计算有效词元(非填充词元)的损失,通过掩码屏蔽填充项。
- 训练流程:
- 输入源序列和目标序列(含
<bos>和<eos>)。 - 编码器生成上下文向量,解码器根据上下文向量和目标序列的前序词元预测下一词元,计算损失并反向传播优化参数。
- 输入源序列和目标序列(含
代码实现与示例
基于 GRU 的 Seq2Seq 模型实现,核心步骤如下:
-
编码器类(Seq2SeqEncoder):
class Seq2SeqEncoder(d2l.Encoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers):
self.embedding = nn.Embedding(vocab_size, embed_size) # 嵌入层
self.rnn = rnn.GRU(num_hiddens, num_layers) # 多层GRU
def forward(self, X):
X = self.embedding(X).swapaxes(0, 1) # 转换为(时间步, 批量大小, 嵌入维度)
output, state = self.rnn(X) # 输出所有时间步的隐状态和最终状态
return output, state -
解码器类(Seq2SeqDecoder):
class Seq2SeqDecoder(d2l.Decoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers):
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers)
self.dense = nn.Dense(vocab_size) # 输出层预测词元概率
def init_state(self, enc_outputs):
return enc_outputs[1] # 使用编码器的最终状态初始化
def forward(self, X, state):
X = self.embedding(X).swapaxes(0, 1)
context = state[0][-1] # 上下文向量(最后一层的最终状态)
X_and_context = np.concatenate([X, context], axis=2) # 拼接上下文
output, state = self.rnn(X_and_context, state)
output = self.dense(output).swapaxes(0, 1) # 转换为(批量大小, 时间步, 词表大小)
return output, state -
训练与预测:
- 加载预处理后的“英-法”数据集,使用掩码处理填充词元。
- 通过循环神经网络的编码器和解码器进行端到端训练,优化模型参数以最小化翻译损失。
Seq2Seq 的应用与局限
- 优点:
- 端到端学习,无需人工设计规则,适用于复杂语义转换。
- 通过 RNN 捕捉序列中的长期依赖关系。
- 局限:
- 计算效率低:RNN 逐时间步处理,难以并行化,不适用于长序列。
- 上下文向量瓶颈:固定长度的向量可能无法完全捕捉长输入序列的所有信息。
- 后续改进:引入注意力机制(Attention)优化上下文向量的使用(如 Bahdanau Attention),或使用 Transformer 替代 RNN。
束搜索
机器翻译等序列生成任务中常用的三种搜索策略:贪心搜索、穷举搜索和束搜索。 在序列生成任务(如机器翻译)中,解码器需要逐个生成目标词元,每个时间步都有多种可能的选择(如法语中“run”可能对应“cours”或“courez”)。搜索策略的目标是从所有可能的序列中找到最可能的输出序列(即条件概率最高的序列)。
三种搜索策略对比
1. 贪心搜索Greedy Search
- 核心思想:在每个时间步选择当前条件概率最高的词元,直到生成结束符或达到最大长度。
- 例:翻译“I am home”时,每个时间步选当前最优词,如“I”→“je”,“am”→“suis”,“home”→“chez moi”,组合成“je suis chez moi”。
- 优点:计算速度快,每次只考虑当前最优选择,计算量为$O(|Y| \times T')$($|Y|$是词表大小,$T'$是序列长度)。
- 缺点:短视,可能错过全局最优。例如:
- 时间步 1 选 A(概率 0.5),时间步 2 选 B(概率 0.4),但时间步 2 选 C(概率 0.3)可能在后续步骤中得到更高的整体概率(如 0.5×0.3×0.6×0.6=0.054 > 0.5×0.4×0.4×0.6=0.048)。
2. 穷举搜索Exhaustive Search
- 核心思想:穷举所有可能的输出序列,计算每个序列的整体概率,选择最高的一个。
- 优点:理论上能找到最优序列。
- 缺点:计算量爆炸,如词表大小为 1 万,序列长度为 10 时,需计算$10000^{10}$种可能,完全不可行。
3. 束搜索(Beam Search)
- 核心思想:介于贪心和穷举之间的折中策略,通过超参数**束宽(Beam Size,k)**控制每次保留的候选序列数:
- 时间步 1:选 k 个概率最高的词元作为初始候选序列(如 k=2 时选 A 和 C)。
- 后续时间步:对每个候选序列,生成所有可能的下一词元,保留 k 个整体概率最高的新候选序列。
- 结束条件:生成结束符或达到最大长度后,从所有候选中选最优序列(考虑长度惩罚,避免偏向短序列)。
- 优点:平衡精度和速度,计算量为$O(k \times |Y| \times T')$,k=1 时退化为贪心搜索。
- 缺点:需调参(束宽 k),k 越大精度越高但速度越慢,一般为 5-10。
总结
- 束搜索的核心优势:通过调整束宽 k,在合理计算成本下显著提升精度,是实际应用中的主流选择。
- 长度惩罚:公式$\frac{1}{L^\alpha} \sum \log P$用于平衡序列长度和概率,避免模型偏向生成过短或过长的序列(α 通常取 0.75)。
序列模型
股价波动、用户行为、文本语句等都是序列数据,其特点是前后数据相互关联,顺序不能打乱。序列数据的时间依赖性**使得传统机器学习模型难以处理,需专门的统计工具和神经网络架构。
统计工具:自回归与隐变量模型
AR自回归模型Autoregressive Models
- 思路:用最近的 τ 个历史数据预测当前值,如用前 4 天股价预测第 5 天股价。
- 公式:$( x_t \sim P(x_t \mid x_{t-1}, \dots, x_{t-\tau}) )$
- 优点:参数固定,可训练深度网络;缺点:仅依赖近期数据,可能忽略长距离依赖。
隐变量自回归模型Latent Autoregressive Models
- 思路:引入“隐状态”(如“市场情绪”)总结历史信息,用隐状态更新预测。
- 公式:
- 预测:$( \hat{x}_t = P(x_t \mid h_t) )$
- 隐状态更新:$( h_t = g(h_{t-1}, x_{t-1}) )$
- 优点:能捕捉更复杂的时间依赖;缺点:隐状态不可观测,需假设其动态变化。
- 公式:
马尔可夫模型(Markov Models)
- 简化假设:当前状态仅依赖前一状态(一阶马尔可夫性),如$( P(x_t \mid x_{t-1}, \dots, x_1) = P(x_t \mid x_{t-1}) )$。
- 应用场景:离散数据(如文本分词),可通过动态规划高效计算概率。
因果关系
预测分析:单步与多步预测的差异
- 内插 vs 外推:内插(已知范围内估计)较简单,外推(超出范围预测)需考虑时间动态变化,难度大。
- 模型选择:自回归模型适用于短期依赖,隐变量模型(如后续章节的 RNN)更适合捕捉长期依赖。
单步预测One-Step Prediction
- 定义:用历史数据预测下一时刻的值(k=1)。
- 效果:模型在训练数据外的预测仍较准确,因每步依赖真实历史数据,误差未累积。
多步预测Multi-Step Prediction
- 定义:用历史数据和之前的预测值递归预测未来多步(如 k=64)。
- 问题:
- 误差累积:每步预测误差会传递到下一步,导致长距离预测严重偏离(如 64 步预测趋近于常数)。
- 示例:天气预报中,24 小时内较准,超过则精度骤降。
文本预处理
文本预处理的必要性
- 计算机的“语言障碍”:
计算机只能处理数字,而文本是字符串形式(如英文单词、汉字),需要先“翻译”成数字索引。
- 例如:“机器”→ 1,“学习”→ 2,这样模型才能理解和计算。
- 核心目标:将文本转换为有序的数字序列,同时保留语义信息,减少噪声和冗余。
预处理步骤详解
1. 读取数据集
从文件中读取文本内容,存储为字符串列表。 示例:加载《时间机器》小说文本,共 3221 行。预处理:用正则表达式去除非字母字符(如标点符号),统一转换为小写字母。
-
代码演示:
def read_time_machine():
with open('timemachine.txt', 'r') as f:
lines = f.readlines()
# 去除非字母字符,转小写,去首尾空格
return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]
2. 词元化Tokenization
-
定义:将文本拆分成最小语义单元(词元),可以是单词或字符。
- 单词级词元化:按空格拆分,如“the time machine”→ ['the', 'time', 'machine']。
- 字符级词元化:拆分成单个字符,如“abc”→ ['a', 'b', 'c']。
-
代码演示:
def tokenize(lines, token='word'):
if token == 'word':
return [line.split() for line in lines] # 按单词拆分
elif token == 'char':
return [list(line) for line in lines] # 按字符拆分
tokens = tokenize(lines) # 得到词元列表的列表
3. 构建词表Vocabulary
-
作用:将词元映射到唯一的数字索引,便于模型输入。
-
步骤:
- 统计词频:计算每个词元在语料中出现的频率。
- 过滤低频词:丢弃出现次数少于阈值(如 min_freq=1)的词元,减少词表大小。
- 分配索引:
- 保留特殊词元:未知词元(,索引 0)、填充词元()等。
- 按词频排序,高频词优先获得低索引(如“the”→ 1,“machine”→ 2)。
-
代码演示:
class Vocab:
def __init__(self, tokens, min_freq=0, reserved_tokens=None):
counter = collections.Counter(tokens) # 统计词频
# 按频率从高到低排序,保留高频词
self.idx_to_token = ['<unk>'] + (reserved_tokens or [])
self.token_to_idx = {token: idx for idx, token in enumerate(self.idx_to_token)}
for token, freq in sorted(counter.items(), key=lambda x: -x[1]):
if freq >= min_freq and token not in self.token_to_idx:
self.idx_to_token.append(token)
self.token_to_idx[token] = len(self.idx_to_token) - 1 -
示例:词表中的映射关系: '' → 0,'the' → 1,'time' → 2,'machine' → 3,...
完整流程示例
-
输入原始文本:
"The Time Machine by H.G. Wells" -
读取并清洗:转换为小写,去除标点 → "the time machine by h g wells"。
-
词元化(单词级):拆分为 ['the', 'time', 'machine', 'by', 'h', 'g', 'wells']。
-
构建词表:词表包含这些词元,映射为索引序列 [1, 2, 3, 4, 5, 6, 7]。
-
未知词处理:若出现未登录词(如'hello'),统一映射为 0()。
语言模型和数据集
语言模型
- 简单理解:语言模型是一种计算文本序列概率的模型,用来判断一段文字是否“像人话”。
- 例如:判断“我吃饭”和“饭吃我”哪个更合理,前者概率更高。
语言模型的作用
- 消除歧义:
- 语音识别中,“to recognize speech”和“to wreck a nice beach”发音相似,语言模型可根据语义选择正确的文本。
- 断句问题:“我想吃奶奶” vs “我想吃,奶奶”,后者更符合常理。
- 生成自然文本:
- 基于前文生成合理的后续内容,如聊天机器人、自动写作等。
- 虽然目前模型还不能真正“理解”文本,但能生成语法正确的内容。
训练语言模型
1. 统计方法:从数据中学习概率
- 基本思路:
通过统计语料库中单词和单词组合的频率来估计概率。
- 单词语概率:$( P(\text{deep}) = \frac{\text{“deep”出现次数}}{\text{总单词数}} )$。
- 条件概率(如二元语法):$( P(\text{learning}|\text{deep}) = \frac{\text{“deep learning”出现次数}}{\text{“deep”出现次数}} )$。
- 问题与挑战:
- 低频词问题:罕见单词或组合(如“deep learning is fun”)出现次数少,统计不准确。
- 存储问题:需记录所有单词组合的频率,数据量大时内存不足。
- 语义缺失:无法捕捉单词间的语义关联(如“猫”和“猫科动物”)。
- 解决方案:拉普拉斯平滑 给低频词的计数添加一个小常数,避免零概率问题。例如:$P(\text{x}) = \frac{n(\text{x}) + \epsilon}{n + m\epsilon} \quad (\epsilon \text{是平滑参数,} m \text{是单词种类数})$
2. 马尔可夫模型与 n 元语法
- 马尔可夫假设:
假设当前词只依赖前 k 个词(k 阶马尔可夫链),简化计算。
- 一元语法(unigram):独立假设,$( P(x_1, x_2) = P(x_1)P(x_2) )$(不考虑上下文)。
- 二元语法(bigram):依赖前一个词,$( P(x_2|x_1) )$(如“吃饭”中“饭”依赖“吃”)。
- 优缺点:
- 优点:计算复杂度随 k 增长可控(k=3 时只需记录三个词的组合)。
- 缺点:k 较大时仍需大量数据,且无法捕捉长距离依赖(如段落级上下文)。
RNN循环神经网络
传统神经网络的局限无法捕捉序列数据中的时间依赖关系(如前后单词的顺序影响),为此诞生了RNN,通过隐状态捕捉上下文。
循环神经网络(RNN)的核心创新:隐状态(记忆机制)
Recurrent Neural Network
- 隐状态的作用:
RNN 引入“隐状态”(记作$( h_t )$)来存储过去序列的信息,允许当前时间步的计算依赖于前序步骤的结果。
- 例如:预测“我吃饭”的下一个词时,$( h_t )$会记录“我”和“吃”的信息,帮助判断下一个词更可能是“饭”而非“书”。
- 计算逻辑:
- 当前时间步的隐状态$( h_t )$由两部分决定:
- 当前输入$( X_t )$(如当前词的特征);
- 前一时间步的隐状态$( h_{t-1} )$(如之前词的上下文信息)。
- 公式:$( h_t = \phi(X_t W_{xh} + h_{t-1} W_{hh} + b_h) )$,其中$( \phi )$是激活函数(如 ReLU),$( W_{xh} )$和$( W_{hh} )$是权重矩阵,用于融合输入和历史信息。
- 当前时间步的隐状态$( h_t )$由两部分决定:
- 参数共享机制:
不同时间步共享同一组权重参数($( W_{xh}, W_{hh} )$等),避免了参数随时间步增长的问题,大幅降低计算复杂度。


RNN 的结构与计算流程
- 展开的时间维度:
RNN 在时间轴上展开后,每一步的计算逻辑相同,但隐状态会逐步积累序列信息。
- 例如:处理“machine”序列时,每个字符(m, a, c, h, i, n)依次输入,隐状态$( h_t )$逐渐包含整个前缀的信息,用于预测下一个字符(如“m”→“a”,“ma”→“c”等)。
- 输入与输出:
- 输入:每个时间步的词元(如字符)通过嵌入层转换为向量($( X_t )$)。
- 输出:通过全连接层将隐状态映射为词表上的概率分布(如预测下一个字符的概率)。
- 示例:输入序列“machin”,标签序列为“achine”,模型通过学习每个位置的条件概率(如 P('a'|'m'), P('c'|'ma'), 等)生成下一个字符。
字符级语言模型:用 RNN 生成文本
- 任务定义:
根据前序字符预测下一个字符,属于序列生成问题。
- 例如:输入“hel”,模型输出“lo”的概率较高,生成“hello”。
- 训练方法:
- 数据预处理:将文本拆分为字符序列,移位后作为输入-标签对(如输入“abcd”,标签“bcde”)。
- 损失函数:交叉熵损失,衡量预测概率与真实标签的差异。
- 优化目标:最小化困惑度(Perplexity),其定义为平均交叉熵损失的指数,值越小表示模型预测越准确。
- 完美模型的困惑度为 1,随机猜测模型的困惑度等于词表大小。
困惑度(Perplexity):评估语言模型的指标
- 直观理解:
衡量模型预测下一个词元的“不确定性”,等价于“平均可选词元数”。
- 示例:
- 困惑度=1:模型完全确定下一个词元(如 P(‘a’|‘h’) = 1)。
- 困惑度=1000:模型预测等价于从 1000 个词元中随机选择。
- 示例:
- 作用:
用于比较不同模型的性能,例如:
- RNN 的困惑度低于 n 元语法模型,说明其捕捉依赖关系的能力更强。
- 字符级模型的困惑度通常高于单词级模型,因字符的语义信息更少。
RNN 的优势与局限
- 优势: 能捕捉序列中的时间依赖,适合处理文本、语音等时序数据。 参数共享机制使其适用于长序列,避免维度灾难。
- 局限:
- 长期依赖问题:隐状态随时间传递时可能丢失早期信息。
- 计算效率:每个时间步需等待前一步完成,难以并行处理。
循环神经网络的从零开始实现
准备工作:数据预处理与编码
- 数据加载与清洗: 以《时间机器》文本为例,加载数据后去除标点符号并转为小写,拆分为字符序列。例如,原文“Hello!”→“hello”。
- 独热编码(One-Hot Encoding):
将每个字符转换为唯一的二进制向量(如字符“a”→[1,0,0,...],“b”→[0,1,0,...]),便于神经网络处理。
- 缺点:词表大时向量维度高(如 26 个字母需 26 维),且无法捕捉字符间语义关联。
模型构建:从参数初始化到前向传播
- 参数初始化: 定义隐藏层和输出层的权重矩阵($W_{xh}, W_{hh}, W_{hq}$)和偏置($b_h, b_q$),随机初始化并附加梯度以便训练。
- 隐状态初始化: 初始隐状态为全零张量,形状为(批量大小,隐藏单元数),用于存储序列的历史信息。
- 前向传播逻辑:
- 对每个时间步的输入(独热向量),结合前一隐状态计算当前隐状态: $$h_t = \tanh(X_t W_{xh} + h_{t-1} W_{hh} + b_h)$$
- 通过输出层将隐状态转换为字符概率分布: $$o_t = h_t W_{hq} + b_q$$
- 示例:输入“time”,逐个字符计算隐状态,最终输出“t”“i”“m”“e”的预测概率。
模型训练:从预测到梯度优化
- 预测函数(预热与生成):
- 预热期:输入前缀字符(如“time”),更新隐状态但不输出,使模型“理解”上下文。
- 生成期:基于预热后的隐状态,逐字符预测后续内容(如生成“traveller”)。
- 梯度裁剪(Gradient Clipping):
- 原因:长序列反向传播时梯度可能爆炸(数值不稳定)。
- 方法:将梯度范数限制在阈值内(如 θ=1),避免参数更新过大导致模型发散。
- 训练循环:
- 随机采样或顺序划分数据,前者每次随机截断序列(需重新初始化隐状态),后者保留相邻序列的隐状态连续性。
- 使用交叉熵损失衡量预测与真实字符的差异,通过随机梯度下降(SGD)优化参数。
- 评估指标:困惑度(Perplexity),值越小表示预测越准确(完美模型为 1)。
通过时间反向传播
什么是通过时间反向传播(BPTT)
- 本质:它是反向传播算法在循环神经网络(RNN)中的应用,用于计算模型参数的梯度。
- 原理:将 RNN 按时间步展开成一个链式结构(类似多层神经网络),然后从最后一个时间步开始,反向计算每个参数的梯度。
- 目标:通过链式法则,计算损失函数对所有参数(如隐藏层权重$W_{hx}$、$W_{hh}$,输出层权重$W_{qh}$)的梯度,以便进行参数更新。
RNN 的梯度计算难题:梯度消失/爆炸
- 问题根源:RNN 的隐状态$h_t$依赖于前一个时间步的隐状态$h_{t-1}$,导致梯度计算时出现 矩阵的高次幂(如$W_{hh}^{\top}$的幂次)。
- 若矩阵特征值 小于 1,梯度会随时间步长指数级衰减(梯度消失);
- 若特征值 大于 1,梯度会指数级增长(梯度爆炸)。
- 影响:长序列(如 1000 个时间步)的梯度计算在计算上不可行(耗时耗内存),且数值不稳定,导致模型难以训练。
解决方案:截断反向传播
为解决长序列梯度计算的难题,常见方法是截断时间步长,仅计算最近若干步的梯度:
- 常规截断(固定长度截断)
- 将序列分割为固定长度的子序列(如每 50 步一段),对每个子序列独立进行反向传播。
- 优点:计算量大幅减少,数值稳定性提高;
- 缺点:忽略长距离依赖,模型更关注短期信息。
- 随机截断
- 随机决定截断的时间步长(用概率$π_t$控制是否终止反向传播),长序列出现概率低但权重更高。
- 理论优势:可能捕获部分长距离依赖;
- 实际问题:方差较大,效果不一定优于常规截断。
- 完全计算(仅理论探讨)
- 直接计算所有时间步的梯度,但仅适用于极短序列,实际中不可行(计算量爆炸)。
 ## 改进的循环神经网络
## 改进的循环神经网络
门控循环单元 GRU
门控循环单元(GRU)——一种改进的循环神经网络(RNN),旨在解决传统 RNN 中梯度消失、长期依赖等问题。
为什么需要 GRU
传统 RNN 在处理长序列时存在两个大问题:
- 梯度消失/爆炸:远距离的前后数据关联难以捕捉(比如“我早上吃了饭,所以现在不饿”中,“早上”和“现在”的关联)。
- 无法选择性记忆:对所有数据同等处理,无法忽略无关信息(如文本中的噪声符号)或重置状态(如章节切换时)。
GRU 通过引入门控机制解决这些问题,让模型能自动选择记忆或遗忘哪些信息。
GRU 的核心:两个“门”
GRU 有两个关键门控,均为 0 到 1 之间的向量(通过神经网络学习得到):
- 重置门(Reset Gate)
- 作用:控制“忘记多少过去的隐状态”。
- 通俗理解:
- 当重置门接近 1 时,保留过去的隐状态,类似传统 RNN。
- 当重置门接近 0 时,忽略过去的隐状态,只关注当前输入(比如遇到新章节时,重置状态)。
- 应用场景:捕捉短期依赖(如一句话中的前后词关联)。
- 更新门(Update Gate)
- 作用:控制“保留多少旧隐状态”和“引入多少新候选隐状态”。
- 通俗理解:
- 当更新门接近 1 时,几乎保留全部旧隐状态,忽略当前输入(比如长期记忆的重要信息,如“出生年份”对后续年龄计算的影响)。
- 当更新门接近 0 时,用新候选隐状态完全替换旧状态(比如处理新的无关内容时,清空旧记忆)。
- 应用场景:捕捉长期依赖(如跨段落的主题关联)。
GRU 的工作流程
- 计算门控: 输入当前数据和前一时刻的隐状态,通过神经网络生成重置门(R)和更新门(Z)。
- 生成候选隐状态: 根据重置门决定是否“擦除”旧隐状态,再结合当前输入生成新的候选隐状态(类似传统 RNN 的隐状态更新,但受重置门控制)。
- 更新隐状态: 通过更新门对旧隐状态和候选隐状态进行“混合”,得到最终的新隐状态。
- 公式直观理解:
新隐状态 = 旧隐状态 * 更新门 + 候选隐状态 * (1 - 更新门)(相当于在旧状态和新状态之间选一个“比例”)
- 公式直观理解:

长短期记忆网络 LSTM
长短期记忆网络(LSTM)——一种经典的循环神经网络(RNN)变体,专门用于解决传统 RNN 在处理长序列时的梯度消失和长期依赖问题。
为什么需要 LSTM
传统 RNN 的隐状态更新机制会导致:
- 远距离信息丢失:比如“我 5 岁学会游泳,现在 30 岁仍擅长”中,“5 岁”和“30 岁”的关联难以捕捉。
- 无法选择性遗忘:对所有信息一视同仁,无法主动丢弃噪声(如文本中的无关符号)。
LSTM 通过引入记忆元(Memory Cell)和三个门控机制,让模型能像人类一样选择性记忆、遗忘或输出信息。
LSTM 的核心:三个“门”和记忆元
1. 记忆元(Cell)
- 作用:相当于“存储仓库”,专门记录长期信息(如“5 岁学会游泳”)。
- 特点:通过门控机制控制数据的写入和读取,避免梯度消失。
2. 三个门控
每个门都是 0 到 1 之间的向量(通过神经网络学习得到),用于控制信息的流动:
(1)遗忘门(Forget Gate)
- 作用:决定“丢弃多少记忆元中的旧信息”。
- 接近 1:保留旧信息(如长期有效的知识);
- 接近 0:丢弃旧信息(如过时的临时数据)。
- 例子:读文章时,遇到新章节,遗忘门会丢弃前一章节的无关细节。
(2)输入门(Input Gate)
- 作用:决定“允许多少新信息写入记忆元”。
- 接近 1:接受新信息(如当前句子的关键词);
- 接近 0:拒绝新信息(如噪声符号)。
- 例子:翻译句子时,输入门只允许有用词汇进入记忆元。
(3)输出门(Output Gate)
- 作用:决定“输出多少记忆元中的信息到隐状态”。
- 接近 1:输出信息用于预测(如生成下一个词);
- 接近 0:保留信息不输出(如暂时用不到的背景知识)。
- 例子:生成文本时,输出门根据当前需求决定是否使用记忆元中的历史信息。
LSTM 的工作流程
- 计算三个门:
- 输入当前数据和前一时刻的隐状态,生成遗忘门(F)、输入门(I)、输出门(O)。
- 生成候选记忆元:
- 根据当前输入和隐状态,生成待写入记忆元的新候选值(类似草稿)。
- 更新记忆元:
- 遗忘阶段:用遗忘门过滤旧记忆元中的信息(
旧记忆 * 遗忘门)。 - 输入阶段:用输入门选择候选记忆元中的新信息(
候选记忆 * 输入门)。 - 合并:旧记忆的保留部分 + 新信息的接受部分 = 新记忆元。
- 遗忘阶段:用遗忘门过滤旧记忆元中的信息(
- 计算隐状态:
- 用输出门控制记忆元的输出:
隐状态 = 输出门 * tanh(新记忆元)。 (tanh 确保值在-1 到 1 之间,输出门决定漏出多少信息)
- 用输出门控制记忆元的输出:

LSTM 与 GRU 的对比
- 门控数量:LSTM 有 3 个门,GRU 有 2 个门(合并了输入门和遗忘门为更新门)。
- 复杂度:LSTM 计算更复杂,但灵活性更高;GRU 更简单,训练速度更快。
- 效果:两者均能解决长期依赖问题,实际应用中根据任务选择(如复杂场景用 LSTM,轻量场景用 GRU)。
深度循环神经网络
深度循环神经网络(深度 RNN),即通过堆叠多个循环层(如 LSTM、GRU 等)来增强模型对复杂序列的建模能力。
为什么需要深度 RNN
- 单层 RNN 的局限:单层 RNN(如简单 RNN、GRU、LSTM)虽然能处理序列数据,但对复杂任务(如长文本语义理解、多尺度时间模式分析)的建模能力有限。
- 例如:分析金融数据时,需要同时捕捉短期波动(分钟级)和长期趋势(季度级),单层网络难以兼顾。
- 深度 RNN 的优势:通过堆叠多层循环层,每一层专注于不同层次的特征,实现“分层抽象”:
- 底层:捕捉局部、短期特征(如文本中的单词搭配)。
- 高层:捕捉全局、长期特征(如文本的主题或情感)。
深度 RNN 的结构与原理
1. 网络架构
- 多层循环层堆叠:每层循环层的隐状态同时传递给下一时间步和下一层循环层
- 例如:第 1 层处理原始输入(如单词向量),第 2 层基于第 1 层的输出进一步提取高层特征。
- 数学表达:第$l$层的隐状态$H_t^{(l)}$由以下公式计算:$$H_t^{(l)} = \phi_l\left( H_t^{(l-1)} W_{xh}^{(l)} + H_{t-1}^{(l)} W_{hh}^{(l)} + b_h^{(l)} \right)$$
- $H_t^{(l-1)}$:当前层的输入(来自上一层的隐状态)。
- $H_{t-1}^{(l)}$:当前层前一时间步的隐状态(循环连接)。
- $\phi_l$:激活函数(如 tanh、sigmoid)。
2. 与单层 RNN 的区别
- 信息流动方向: 除了时间维度的循环连接(横向),还增加了层间的垂直连接,形成“多层流水线”。
- 参数规模: 每层都有独立的权重矩阵(如$W_{xh}^{(l)}$、$W_{hh}^{(l)}$),参数总量随层数增加而显著增长。
实现深度 RNN
1. 框架内置支持
主流深度学习框架(如 PyTorch、TensorFlow)提供了多层循环层的简洁接口,只需指定层数和隐藏单元数:
# 以PyTorch为例,定义两层LSTM
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers=2) # num_layers=2表示两层
2. 训练注意事项
- 计算成本高: 多层循环层会显著增加训练时间和显存占用(例如,两层 LSTM 的计算量约为单层的 2 倍)。
- 梯度消失/爆炸风险: 虽然 LSTM/GRU 缓解了单层的梯度问题,但深层网络仍可能因层间传递导致梯度不稳定,需谨慎初始化参数和选择优化器。
- 超参数调整:
- 层数(num_layers):通常 2-4 层,过多易过拟合。
- 隐藏单元数(num_hiddens):需与层数匹配,避免底层信息不足。
双向循环神经网络
双向循环神经网络(Bi-RNN),核心是解决传统单向 RNN 无法利用未来信息的问题。通过同时运行前向和后向两个 RNN,让模型在每个时间步都能同时获取过去和未来的上下文信息,提升预测准确性。
隐马尔科夫模型的动态规划
双向 RNN 的核心原理
1. 结构设计
- 前向 RNN:从序列起点(左)向右处理数据,捕捉过去信息(如“我”“饿了”)。
- 后向 RNN:从序列终点(右)向左处理数据,捕捉未来信息(如“吃半头猪”)。
- 输出合并:每个时间步的隐状态由前向和后向的隐状态拼接或加权求和得到,输入到输出层进行预测。

2. 数学直观
假设序列为$x_1, x_2, \dots, x_T$:
- 前向隐状态$\vec{h}_t$:依赖$x_1$到$x_t$的信息。
- 后向隐状态$\overleftarrow{h}_t$:依赖$x_T$到$x_t$的信息。
- 最终隐状态$h_t = [\vec{h}_t; \overleftarrow{h}_t]$(拼接),包含双向信息。
3. 与隐马尔可夫模型(HMM)的关联
网页通过 HMM 的动态规划原理说明:
- 传统单向 RNN 类似 HMM 的前向递归(从左到右计算概率)。
- 双向 RNN 则补充了后向递归(从右到左),类似 HMM 中同时利用前向和后向信息优化预测,避免单一方向的信息缺失。
典型应用场景
- 自然语言处理:
- 文本填空、命名实体识别(如区分“Green”是人名还是颜色,需前后文语境)。
- 机器翻译(目标语言生成需同时考虑源语言的前后文)。
- 语音识别:语音信号的上下文依赖(如“xian”可能是“先”或“线”,需前后音素判断)。
- 时间序列预测:若未来数据可获取(如已知部分未来值),双向 RNN 可提升预测精度。
注意事项
-
数据要求: 双向 RNN 需要完整的序列数据(未来信息已知),不适用于实时流式数据(如逐字生成文本时,未来词未知)。
-
框架支持:
主流框架(如 PyTorch、TensorFlow)提供双向 RNN 接口,只需设置 bidirectional=True
# PyTorch示例:双向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers=1, bidirectional=True)
机器翻译与数据集
掌握基本的实践过程
什么是机器翻译
- 定义:将文本从一种语言(源语言,如英语)自动翻译成另一种语言(目标语言,如法语)的过程。
- 历史与方法:
- 早期以统计方法为主(如统计机器翻译,需人工设计规则和模型)。
- 现代主流是神经机器翻译(NMT),基于神经网络端到端学习,无需人工拆解任务。
- 关键挑战: 源语言和目标语言的序列长度、语法结构不同,需模型捕捉跨语言的语义对应关系。
为什么预处理如此重要
- 模型输入要求:神经网络只能处理数值化的批量数据,预处理将自然语言转换为模型可理解的格式。
- 效率与性能:统一序列长度可加速矩阵运算(如 GPU 并行计算),有效长度避免无效计算(如忽略填充词元的梯度)。
- 后续模型基础:预处理后的数据集是训练编码器-解码器架构(如 Transformer)的基石,直接影响翻译质量。
编码器-解码器架构
编码器-解码器(Encoder-Decoder)架构是处理序列转换问题(如机器翻译)的核心框架。
- 处理变长序列:传统神经网络难以直接处理长度变化的输入输出,编码器-解码器通过“压缩-解压”解决此问题。
- 模块化设计:编码器和解码器可独立设计(如编码器用双向 RNN,解码器用单向 RNN),灵活适配不同任务。
编码器-解码器架构
- 核心思想:将一个长度可变的序列(如英文句子)转换为另一个长度可变的序列(如法语翻译),分为两个阶段:
- 编码器(Encoder):把输入序列“压缩”成一个固定形状的编码状态(类似语义向量)。
- 解码器(Decoder):根据编码状态“解压”生成目标序列(如逐个词生成翻译)。
- 类比场景: 输入:“They are watching.” → 编码器压缩成“他们正在观看”的语义向量 → 解码器生成法语“Ils regardent.”。

编码器:压缩输入序列
-
功能:接收任意长度的输入序列(如单词列表),输出固定长度的编码状态(如向量)。
-
关键特性:
- 隐藏具体实现细节,只需满足“输入序列 → 编码状态”的接口。
- 可使用循环神经网络(RNN)、Transformer 等实现。
-
代码接口(以 PyTorch 为例):
class Encoder(nn.Module):
def __init__(self):
super().__init__()
def forward(self, X): # X是输入序列(如词元ID数组)
raise NotImplementedError # 具体实现由子类完成
解码器:生成目标序列
-
功能:根据编码器的编码状态,逐个生成目标序列的词元(如翻译后的单词)。
-
关键步骤:
- 初始化状态:用编码器输出的编码状态生成解码器的初始状态。
- 逐词生成:每次输入一个词元(如起始符
<bos>)和当前状态,输出下一个词元及更新后的状态,直到生成结束符<eos>。
-
代码接口(以 PyTorch 为例):
class Decoder(nn.Module):
def __init__(self):
super().__init__()
def init_state(self, enc_outputs): # 用编码器输出初始化状态
raise NotImplementedError
def forward(self, X, state): # X是当前输入词元,state是当前状态
raise NotImplementedError # 返回生成的词元及新状态
合并编码器和解码器
-
整体流程:
- 编码器处理输入序列,得到编码状态。
- 解码器用编码状态初始化,逐个生成目标序列词元。
-
代码框架(以 PyTorch 为例):
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder):
super().__init__()
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X): # enc_X是输入序列,dec_X是目标序列(训练时用)
enc_outputs = self.encoder(enc_X) # 编码
dec_state = self.decoder.init_state(enc_outputs) # 初始化解码器状态
return self.decoder(dec_X, dec_state) # 解码生成目标序列- 训练时:dec_X 是目标序列的输入(含
<bos>等符号)。 - 推理时:dec_X 可逐词生成(如先输入
<bos>,再根据输出逐步添加新词元)。
- 训练时:dec_X 是目标序列的输入(含
序列到序列学习
序列到序列(Seq2Seq)模型是编码器-解码器架构的具体实现,用于解决机器翻译等序列转换问题。
Seq2Seq 模型的核心架构
Seq2Seq 模型由**编码器(Encoder)和解码器(Decoder)两部分组成:

- 编码器:
- 功能:将输入序列(如英文句子)转换为一个固定长度的上下文向量(Context Vector),浓缩输入序列的语义信息。
- 实现:
- 输入序列先通过嵌入层(Embedding Layer)转换为词向量。
- 词向量输入到多层 RNN(如 GRU)中,最终输出所有时间步的隐状态,通常取最后一个时间步的隐状态作为上下文向量。
- 示例:输入“They are watching.”,编码器输出一个包含语义的向量(如“他们正在观看”的抽象表示)。
- 解码器:
- 功能:根据编码器的上下文向量,逐个生成目标序列(如法语翻译)的词元。
- 实现:
- 初始化时,用编码器的最后一个隐状态作为解码器的初始隐状态。
- 输入序列的开始符号(
<bos>)和上下文向量,通过多层 RNN 逐词生成目标序列,直到遇到结束符号(<eos>)。
- 示例:根据上下文向量,解码器逐步生成“Ils”“regardent”“.”“”。
关键技术细节
1. 输入输出处理
- 嵌入层:将词元(如单词)转换为连续的特征向量,捕捉词间语义关系(如“run”和“cours”在向量空间中接近)。
- 序列填充与掩码:
- 对不同长度的序列进行填充(如添加
<pad>)使其等长,便于批量训练。 - 使用**掩码(Mask)**忽略填充词元的损失计算,避免无效数据干扰训练。
- 对不同长度的序列进行填充(如添加
2. 上下文向量的传递
- 编码器的最后一个隐状态作为解码器的初始隐状态,将输入序列的全局信息传递给解码器。
- 解码器在每个时间步将当前词向量与上下文向量拼接,指导目标词元的生成。
3. 损失函数与训练
- 损失计算:使用交叉熵损失函数,仅计算有效词元(非填充词元)的损失,通过掩码屏蔽填充项。
- 训练流程:
- 输入源序列和目标序列(含
<bos>和<eos>)。 - 编码器生成上下文向量,解码器根据上下文向量和目标序列的前序词元预测下一词元,计算损失并反向传播优化参数。
- 输入源序列和目标序列(含
代码实现与示例
基于 GRU 的 Seq2Seq 模型实现,核心步骤如下:
-
编码器类(Seq2SeqEncoder):
class Seq2SeqEncoder(d2l.Encoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers):
self.embedding = nn.Embedding(vocab_size, embed_size) # 嵌入层
self.rnn = rnn.GRU(num_hiddens, num_layers) # 多层GRU
def forward(self, X):
X = self.embedding(X).swapaxes(0, 1) # 转换为(时间步, 批量大小, 嵌入维度)
output, state = self.rnn(X) # 输出所有时间步的隐状态和最终状态
return output, state -
解码器类(Seq2SeqDecoder):
class Seq2SeqDecoder(d2l.Decoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers):
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers)
self.dense = nn.Dense(vocab_size) # 输出层预测词元概率
def init_state(self, enc_outputs):
return enc_outputs[1] # 使用编码器的最终状态初始化
def forward(self, X, state):
X = self.embedding(X).swapaxes(0, 1)
context = state[0][-1] # 上下文向量(最后一层的最终状态)
X_and_context = np.concatenate([X, context], axis=2) # 拼接上下文
output, state = self.rnn(X_and_context, state)
output = self.dense(output).swapaxes(0, 1) # 转换为(批量大小, 时间步, 词表大小)
return output, state -
训练与预测:
- 加载预处理后的“英-法”数据集,使用掩码处理填充词元。
- 通过循环神经网络的编码器和解码器进行端到端训练,优化模型参数以最小化翻译损失。
Seq2Seq 的应用与局限
- 优点:
- 端到端学习,无需人工设计规则,适用于复杂语义转换。
- 通过 RNN 捕捉序列中的长期依赖关系。
- 局限:
- 计算效率低:RNN 逐时间步处理,难以并行化,不适用于长序列。
- 上下文向量瓶颈:固定长度的向量可能无法完全捕捉长输入序列的所有信息。
- 后续改进:引入注意力机制(Attention)优化上下文向量的使用(如 Bahdanau Attention),或使用 Transformer 替代 RNN。
束搜索
机器翻译等序列生成任务中常用的三种搜索策略:贪心搜索、穷举搜索和束搜索。 在序列生成任务(如机器翻译)中,解码器需要逐个生成目标词元,每个时间步都有多种可能的选择(如法语中“run”可能对应“cours”或“courez”)。搜索策略的目标是从所有可能的序列中找到最可能的输出序列(即条件概率最高的序列)。
三种搜索策略对比
1. 贪心搜索Greedy Search
- 核心思想:在每个时间步选择当前条件概率最高的词元,直到生成结束符或达到最大长度。
- 例:翻译“I am home”时,每个时间步选当前最优词,如“I”→“je”,“am”→“suis”,“home”→“chez moi”,组合成“je suis chez moi”。
- 优点:计算速度快,每次只考虑当前最优选择,计算量为$O(|Y| \times T')$($|Y|$是词表大小,$T'$是序列长度)。
- 缺点:短视,可能错过全局最优。例如:
- 时间步 1 选 A(概率 0.5),时间步 2 选 B(概率 0.4),但时间步 2 选 C(概率 0.3)可能在后续步骤中得到更高的整体概率(如 0.5×0.3×0.6×0.6=0.054 > 0.5×0.4×0.4×0.6=0.048)。
2. 穷举搜索Exhaustive Search
- 核心思想:穷举所有可能的输出序列,计算每个序列的整体概率,选择最高的一个。
- 优点:理论上能找到最优序列。
- 缺点:计算量爆炸,如词表大小为 1 万,序列长度为 10 时,需计算$10000^{10}$种可能,完全不可行。
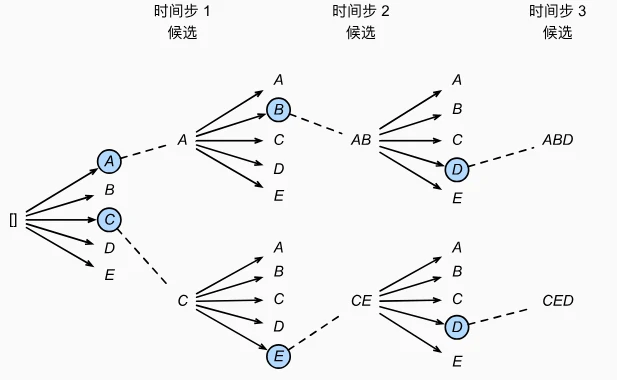
3. 束搜索(Beam Search)
- 核心思想:介于贪心和穷举之间的折中策略,通过超参数**束宽(Beam Size,k)**控制每次保留的候选序列数:
- 时间步 1:选 k 个概率最高的词元作为初始候选序列(如 k=2 时选 A 和 C)。
- 后续时间步:对每个候选序列,生成所有可能的下一词元,保留 k 个整体概率最高的新候选序列。
- 结束条件:生成结束符或达到最大长度后,从所有候选中选最优序列(考虑长度惩罚,避免偏向短序列)。
- 优点:平衡精度和速度,计算量为$O(k \times |Y| \times T')$,k=1 时退化为贪心搜索。
- 缺点:需调参(束宽 k),k 越大精度越高但速度越慢,一般为 5-10。

总结
- 束搜索的核心优势:通过调整束宽 k,在合理计算成本下显著提升精度,是实际应用中的主流选择。
- 长度惩罚:公式$\frac{1}{L^\alpha} \sum \log P$用于平衡序列长度和概率,避免模型偏向生成过短或过长的序列(α 通常取 0.75)。