跳到主要内容

CNN神经网络

卷积神经网络​

从全连接层到卷积​

全连接层的缺点：参数爆炸​

  • 场景引入：比如用多层感知机给百万像素的猫狗照片分类，输入层有 100 万像素，即使隐藏层只有 1000 个神经元，仅这一层就需要 10 亿个参数（100 万 ×1000）。
  • 问题核心：参数太多，训练起来需要大量数据、算力和时间，几乎不可行。
  • 关键原因：全连接层假设所有像素之间都有关系，但图像其实有 “局部性” 和 “平移不变性”，全连接层没有利用这些特性。

卷积神经网络的两大核心原理​

  1. 平移不变性：位置无关，特征不变
  • 类比理解：就像找 “沃尔多”（图 6.1.1），不管他出现在图片哪个位置，他的红条纹衣服、眼镜等特征不变。
    • 卷积神经网络用一个 “特征检测器”（卷积核）扫描全图，只要某个区域出现目标特征，检测器就会响应，不管这个区域在图片左上角还是右下角。
  • 数学意义：同一个卷积核（权重）在图像的所有位置共享，不随位置改变而变化，大幅减少参数数量。
  1. 局部性：只关注相邻区域，不操心远处
  • 现实依据：图像中物体的特征通常由局部像素组成（比如眼睛由周围几个像素的明暗构成），不需要关注整个图像的所有像素。
  • 具体做法：卷积核只处理某个固定大小的局部区域（如 3×3 像素的窗口），每个隐藏单元只与输入图像的局部区域相连，而非全部像素。
  • 效果：进一步减少参数，同时保留关键局部特征。

卷积的数学本质与实际应用​

假设你有两个函数（或数组）：

  • 函数 f：代表原始信号（如图像的像素值）。
  • 函数 g：代表一个 “过滤器”（如卷积核，用于提取特征）。 卷积的核心步骤：
  1. 翻转过滤器：先将 g 函数左右、上下翻转（数学定义要求，实际应用中可能直接使用未翻转的核，结果称为 “互相关”，但深度学习中常统称 “卷积”。）
  2. 滑动窗口：将翻转后的 g 逐行、逐列滑动到 f 的每个位置上。
  3. 相乘求和：在每个位置，将 g 与 f 重叠区域的对应元素相乘，再将结果相加，得到一个新值。 例子（离散数据，二维图像）：
  • 输入图像（3×3 像素）：
  0 1 2
  3 4 5
  6 7 8
  • 卷积核（2×2，未翻转时）：
  0 1
  2 3
  • 翻转后的卷积核：
  3 2
  1 0
  • 计算左上角第一个输出值： 翻转后的核与图像左上角 2×2 区域重叠： 
    0*3 + 1*2 + 3*1 + 4*0 = 0 + 2 + 3 + 0 = 5
  • 输出图像（2×2 像素）：
  5 11
  23 24
卷积在深度学习中充当特征提取器​

在卷积神经网络（CNN）中，卷积操作的目标不是数学意义上的信号分析，而是自动提取数据中的特征，具体特点如下：

  1. 局部感知：只看周围一小片区域
  • 卷积核的大小通常远小于输入图像（如 3×3、5×5），每次只处理图像中的一个局部窗口（如边缘、纹理），而非整个图像。
  • 类比：就像用放大镜观察照片，每次只关注局部细节（如猫的胡须），再通过多层卷积组合成整体特征（如猫的头部）。
  1. 权重共享：一个核用遍全图
  • 同一个卷积核的所有参数在图像的所有位置共享，不会因位置不同而改变。
  • 好处：大幅减少参数数量。例如，一个 3×3 的卷积核在 100×100 的图像上滑动，只需学习 9 个参数，而非 100×100 个参数。
  1. 多通道处理：同时提取多维度特征
  • 彩色图像有 RGB 三个通道（红、绿、蓝），卷积核会为每个通道单独设计权重，再将结果相加，输出新的 “特征图”。
  • 类比：相当于用不同滤镜（如边缘滤镜、颜色滤镜）同时处理图像，每个滤镜输出一个特征图，代表图像某方面的信息。

卷积层的优势：更少参数，更高效率​

  • 对比全连接层：
    • 假设卷积核大小为 3×3，输入通道 3，输出通道 10，那么参数仅为 3×3×3×10=270 个，远少于全连接层的数十亿参数。
  • 归纳偏置的作用：
    • 卷积神经网络利用图像的 “先验知识”（平移不变和局部性），称为 “归纳偏置”。如果这些假设符合现实（如自然图像），模型能更快收敛，泛化能力更强；但若假设不成立（如非平移不变的数据），可能效果不佳。

延伸思考​

  • 如果卷积核大小为 0（Δ=0），相当于每个像素独立处理，类似全连接层（但通道独立）。
  • 平移不变性的缺点：如果物体在不同位置有不同含义（如文字顺序），可能不适用。
  • 图像边界问题：边缘像素的局部窗口可能超出图像范围，需考虑填充（padding）或忽略。
  • 卷积在音频、文本中的应用：音频是一维信号（时间序列），可使用一维卷积；文本是序列数据，一维卷积可提取 n-gram 特征（如 “你好”“世界” 等相邻词语的组合）。

图像卷积​

CNN识别数字6神经网络示例图.webp

互相关运算：卷积层的核心操作​

  • 什么是互相关？ 互相关是卷积层的实际运算过程，简单来说就是用一个卷积核（小窗口）在输入图像上滑动，每次滑动时将窗口内的图像像素与卷积核对应位置的数值相乘，再把结果相加，得到一个输出值。
    • 例子：如图 6.2.1 所示，输入是 3×3 的图像，卷积核是 2×2 的矩阵。当卷积核从左上角开始滑动时，第一个输出值计算为： 0×0 + 1×1 + 3×2 + 4×3 = 19，依次滑动得到最终的 2×2 输出矩阵。
  • 输出大小的计算 输出图像的尺寸会比输入小，计算公式为： (输入高度 - 卷积核高度 + 1) × (输入宽度 - 卷积核宽度 + 1)。 例如，3×3 输入用 2×2 卷积核，输出是 2×2（3-2+1=2）。

卷积层：带参数的互相关运算​

  • 卷积层的组成 卷积层由卷积核权重和偏置两个可学习的参数组成。

    • 权重：即卷积核的数值，通过训练学习得到，用于提取特征。
    • 偏置：一个额外的常数，用于调整输出值，类似全连接层的偏置。

  • 代码实现 用 Python 代码定义了一个简单的卷积层Conv2D，通过corr2d函数实现互相关运算，再加上偏置得到输出。例如：

    class Conv2D(nn.Module):
        def __init__(self, kernel_size):
            super().__init__()
            self.weight = nn.Parameter(torch.rand(kernel_size))  # 随机初始化卷积核权重
            self.bias = nn.Parameter(torch.zeros(1))  # 偏置初始化为0

        def forward(self, x):
            return corr2d(x, self.weight) + self.bias  # 互相关运算+偏置

边缘检测：卷积层的简单应用​

  • 目标：检测图像中颜色变化的边缘 构造一个黑白图像（中间四列为黑色，其余为白色），用一个简单的卷积核[1, -1]检测垂直边缘。
    • 原理：当卷积核滑过图像时，如果相邻像素值不同（如白 → 黑或黑 → 白），输出非零值；如果相同（如白 → 白），输出 0。
    • 结果：输出图像中，1表示白 → 黑的边缘，-1表示黑 → 白的边缘，其余为 0（如图 6.2.3 所示）。
  • 局限性 该卷积核只能检测垂直边缘，无法检测水平边缘。若将图像转置后再用同样的卷积核运算，输出全为 0，说明卷积核具有方向性。

学习卷积核：从数据中自动优化参数​

  • 为什么需要学习卷积核？ 手动设计复杂的卷积核（如检测多种特征）非常困难，因此可以通过训练让模型自动学习卷积核权重。
    • 方法：
      1. 随机初始化卷积核权重。
      2. 计算预测输出与真实输出的误差（如均方误差）。
      3. 通过反向传播更新权重，减小误差。

填充和步幅​

为什么需要填充和步幅​

  • 填充的目的： 当使用卷积核处理图像时，输出尺寸会变小（例如 3×3 输入用 2×2 卷积核，输出 2×2），导致边缘像素丢失。填充就是在图像周围添加一圈 “边缘”（通常是 0），避免信息丢失，同时可以控制输出尺寸与输入相同。
  • 步幅的目的： 控制卷积核滑动的步长。步幅为 1 时，卷积核每次移动 1 个像素；步幅为 2 时，每次移动 2 个像素，可快速降低图像尺寸，减少计算量。

填充：给图像加 “边框”​

  • 什么是填充？ 在图像的上下左右边缘添加若干行 / 列的像素（通常填 0），使得卷积后的输出尺寸更大。

  • 填充如何影响输出尺寸？ 设输入尺寸为$(n_h \times n_w)$，卷积核尺寸$(k_h \times k_w)$，上下填充$p_h$行，左右填充$p_w$列，则输出尺寸为：$(n_h - k_h + p_h + 1) \times (n_w - k_w + p_w + 1)$

    • 保持输出与输入同尺寸：当$(p_h = k_h - 1)$且$(p_w = k_w - 1)$时，输出尺寸等于输入尺寸。例如，3×3 输入用 3×3 卷积核，填充 1 圈 0，输出仍为 3×3。
    • 奇数卷积核的优势：常用奇数卷积核（如 3×3、5×5），因为可以在上下 / 左右填充相同行数 / 列数，保持对称（如 3×3 核填充 1 行 / 列，两边各加 0.5 行 / 列，实际取整后对称）。

  • 代码示例：

    # 用3×3卷积核，填充1行/列，输入8×8，输出8×8
    conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
    X = torch.rand(8, 8)
    print(comp_conv2d(conv2d, X).shape)  # 输出: torch.Size([8, 8])

步幅：大步滑动卷积核​

  • 什么是步幅？ 卷积核在图像上滑动的间隔距离。步幅为 1 时，每次移动 1 个像素；步幅为 2 时，每次跳过 1 个像素，直接移动 2 个像素。

    • 例子：5×5 输入用 2×2 卷积核，步幅 3，输出尺寸为 2×2（滑动时超出边界则停止）。

  • 步幅如何影响输出尺寸？ 设垂直步幅$s_h$，水平步幅$s_w$，则输出尺寸为：$(\left\lfloor \frac{n_h - k_h + p_h + s_h}{s_h} \right\rfloor \times \left\lfloor \frac{n_w - k_w + p_w + s_w}{s_w} \right\rfloor)$

    • 简化情况：若填充$(p_h = k_h - 1)$，$(p_w = k_w - 1)$，则输出尺寸约为$(\frac{n_h}{s_h} \times \frac{n_w}{s_w})$（若能整除）。例如，8×8 输入，步幅 2，输出 4×4。
    # 步幅2，输入8×8，输出4×4
    conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
    print(comp_conv2d(conv2d, X).shape)  # 输出: torch.Size([4, 4])

填充和步幅的组合应用​

  • 灵活调整尺寸：
    • 填充用于保留边缘信息或扩大尺寸，步幅用于快速降维。
    • 例如：输入 240×240，用 5×5 卷积核，填充 2，步幅 3，则输出尺寸为：$(\frac{240 - 5 + 2 \times 2 + 3}{3} = 80 \quad \Rightarrow \quad 80 \times 80)$
  • 奇数核 + 对称填充 + 步幅 1： 这是最常见的组合（如 ResNet 等模型），可确保输出与输入同尺寸，且卷积核中心对准输入像素，便于特征对齐。

多输入和多输出通道​

通道是什么​

  • 类比理解：
    • 通道就像图像的 “维度扩展”。例如，彩色照片有 RGB 三个通道（红、绿、蓝），每个通道是一个二维像素矩阵，合起来组成三维张量（高度 × 宽度 × 通道数）。
    • 在神经网络中，每个通道可以理解为一个 “特征探测器”，负责提取不同的信息（如边缘、纹理、颜色等）。
  • 数学表示：
    • 输入图像的通道数记为$(c_i)$（如 RGB 图像$(c_i=3)$），输出通道数记为$(c_o)$（由卷积核数量决定）。
    • 卷积核的形状为$(c_o \times c_i \times k_h \times k_w)$，其中$(k_h \times k_w)$是空间窗口大小。

多输入通道：处理彩色图像​

  • 核心逻辑： 当输入有多个通道时，卷积核必须有相同的输入通道数，每个通道分别进行互相关运算，再将结果相加。

    • 例子：输入是 2 通道的图像，卷积核也有 2 个通道（每个通道是 2×2 的矩阵）。计算时，每个输入通道与对应的卷积核通道相乘求和，最后将两个通道的结果相加，得到单通道的输出。

  • 代码实现：

    def corr2d_multi_in(X, K):
        # X和K按通道遍历，每个通道做互相关后求和
        return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

    其中，X 是输入张量（形状为$(c_i \times h \times w)$），K 是卷积核张量（形状为$(c_i \times k_h \times k_w)$）。

多输出通道：提取多种特征​

  • 核心逻辑： 每个输出通道对应一个独立的卷积核，每个卷积核在所有输入通道上运算，输出一个特征图。多个卷积核的结果叠加，形成多通道输出。

    • 例子：使用 3 个卷积核，每个核的形状为$(2 \times 2 \times 2)$（2 输入通道，2×2 空间窗口），输出就是 3 通道的特征图，每个通道对应一种特征（如边缘、纹理、颜色）。

  • 代码实现：

    def corr2d_multi_in_out(X, K):
        # 对每个卷积核（输出通道）单独计算，再堆叠结果
        return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

    其中，K 的形状为$(c_o \times c_i \times k_h \times k_w)$，每个 k 是一个输出通道对应的卷积核。

1×1 卷积：升降维​

  • 表面矛盾： 1×1 卷积核的空间窗口只有 1×1 像素，无法提取相邻像素的空间特征，那它有什么用？

  • 实际作用：

    1. 通道升降维,仅改变通道数而不改变空间特征：
      • 例如，输入是 256 通道，使用 1×1 卷积核（输出通道 64），可将通道数压缩为 64，减少后续计算量（会损失信息）。
    2. 跨通道交互：
      • 在每个像素位置，1×1 卷积相当于一个全连接层，将多个输入通道的信息线性组合成新的输出通道。
      • 例如，输入 3 通道，输出 2 通道，每个输出像素是输入同位置 3 个通道的加权和（类似全连接层的矩阵乘法）。

  • 数学本质： 1×1 卷积的计算等价于对每个像素的通道维度做全连接变换。假设输入形状为$(c_i \times h \times w)$，卷积核形状为$(c_o \times c_i \times 1 \times 1)$，则运算可拆解为：

    def corr2d_multi_in_out_1x1(X, K):
        c_i, h, w = X.shape
        c_o = K.shape[0]
        # 将每个像素的通道展平为向量，与卷积核做矩阵乘法
        X = X.reshape((c_i, h * w))  # 形状：[c_i, h*w]
        K = K.reshape((c_o, c_i))    # 形状：[c_o, c_i]
        Y = torch.matmul(K, X)       # 矩阵乘法，形状：[c_o, h*w]
        return Y.reshape((c_o, h, w))

汇聚层​

汇聚层的核心作用：让特征更鲁棒、降低计算量​

  • 类比理解： 假设你在看一张猫的照片，汇聚层就像用放大镜观察局部区域后 “总结” 出关键点（比如 “这里有胡须”），而不是关注每个像素的精确位置。这样即使猫的位置稍微移动，依然能识别出关键特征。
  • 两大目标：
    1. 平移不变性：减少模型对物体位置的敏感性（如猫在图片左或右都能被识别）。
    2. 降采样：降低特征图的空间尺寸（如从 100×100→50×50），减少计算量，同时保留主要特征。

最大汇聚层 vs 平均汇聚层：如何 “总结” 区域特征​

最大汇聚层​

  • 操作：在每个固定大小的窗口（如 2×2）中，取所有像素的最大值作为输出。

    • 例子：输入矩阵：

      0 1 2
      3 4 5
      6 7 8

      用 2×2 窗口做最大汇聚，第一个窗口（左上角）的最大值是 4（0,1,3,4 中的最大值），最终输出：

      4 5
      7 8

  • 适用场景：提取突出特征（如边缘、斑点），因为最大值能保留最显著的信息。

平均汇聚层​

  • 操作：在窗口中计算所有像素的平均值作为输出。

    • 例子：上述输入的 2×2 窗口平均值为：第一个窗口平均值 =(0+1+3+4)/4=2，输出：

      2 3
      5 6

  • 适用场景：平滑特征，减少噪声影响，适用于背景复杂的图像。

填充和步幅：控制输出尺寸的关键​

  • 填充（Padding）

    ：在输入边缘添加空白（通常为 0），避免边缘特征被忽略，同时控制输出尺寸。

    • 例子：输入 4×4，汇聚窗口 3×3，填充 1 圈 0 后，输出仍为 4×4（否则为 2×2）。

  • 步幅（Stride）

    ：汇聚窗口滑动的间隔。步幅越大，输出尺寸越小。

    • 例子：输入 4×4，窗口 2×2，步幅 2，则输出 2×2（窗口每次移动 2 像素）。

  • 公式：输出尺寸 =$\left\lfloor \frac{输入尺寸 - 窗口尺寸 + 2×填充}{步幅} \right\rfloor + 1$。

多通道处理：各通道独立运算​

  • 规则：汇聚层对每个通道单独操作，输出通道数与输入相同。
    • 例子：输入是 2 通道的特征图，每个通道分别进行最大汇聚，输出仍为 2 通道，每个通道的尺寸按窗口和步幅调整。
  • 代码示例： 
    # 输入形状：(批量, 通道, 高度, 宽度)
    X = torch.cat((X, X+1), dim=1)  # 2通道输入
    pool2d = nn.MaxPool2d(3, padding=1, stride=2)
    output = pool2d(X)  # 输出通道数仍为2

汇聚层与卷积层的对比​

层类型参数运算方式输出尺寸影响核心功能
卷积层有权重像素与核的互相关运算由核大小、填充、步幅决定特征提取（空间 + 通道）
汇聚层无参数取窗口内最大值 / 平均值由窗口、填充、步幅决定特征聚合、降维、抗平移

卷积神经网络 LeNet​

1.LeNet 的网络结构：卷积与全连接的结合​

LeNet 的架构分为两部分：卷积编码器（提取图像特征）和全连接层（分类决策），具体如下：

卷积编码器：两层卷积​

  • 第一层卷积：
    • 输入：28×28 的单通道图像（手写数字通常为黑白图像）。
    • 操作：使用 6 个 5×5 的卷积核，填充 2 像素（保持输出尺寸不变），激活函数为 sigmoid。
    • 输出：6 个 28×28 的特征图（通道数增加到 6）。
    • 汇聚：2×2 平均汇聚层，步幅 2，输出变为 6 个 14×14 的特征图（尺寸减半）。
  • 第二层卷积：
    • 操作：16 个 5×5 的卷积核，无填充（输出尺寸减少 4 像素），激活函数为 sigmoid。
    • 输出：16 个 10×10 的特征图。
    • 汇聚：2×2 平均汇聚层，步幅 2，输出变为 16 个 5×5 的特征图（尺寸再次减半）。
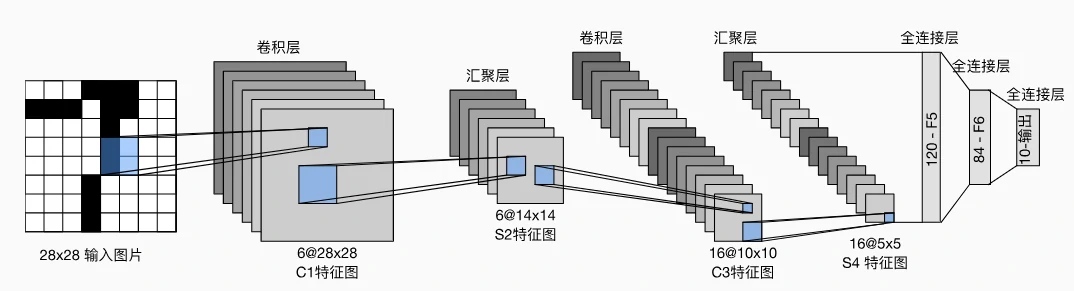
LeNet卷积神经网络架构

全连接层：从特征到分类​

  • 展平操作：将 16 个 5×5 的特征图展平为 16×5×5=400 维的向量。
  • 三层全连接：
    • 第一层：400→120 维，激活函数 sigmoid。
    • 第二层：120→84 维，激活函数 sigmoid。
    • 第三层：84→10 维（对应 10 个数字类别），无激活函数（直接输出分类概率）。

关键特点：

  • 卷积层通过 “空间下采样”（汇聚层）减少尺寸，同时增加通道数（从 1→6→16），逐步提取更复杂的特征（如从边缘到数字形状）。
  • 全连接层将高维特征映射到分类结果，类似传统神经网络的决策过程。

LeNet 的代码实现​

import torch.nn as nn

net = nn.Sequential(
    # 第一层卷积+汇聚
    nn.Conv2d(1, 6, kernel_size=5, padding=2),  # 输入1通道，输出6通道，5x5卷积，填充2
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),       # 2x2平均汇聚，尺寸减半

    # 第二层卷积+汇聚
    nn.Conv2d(6, 16, kernel_size=5),             # 输入6通道，输出16通道，5x5卷积（无填充）
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),       # 尺寸再次减半

    # 全连接层
    nn.Flatten(),                               # 展平为一维向量
    nn.Linear(16*5*5, 120), nn.Sigmoid(),        # 400→120
    nn.Linear(120, 84), nn.Sigmoid(),           # 120→84
    nn.Linear(84, 10)                           # 84→10（分类输出）
)

第七章 改进的卷积神经网络​

深度卷积神经网络 AlexNet​

  • 相比 LeNet，AlexNet 在更大数据集上表现更优，证明了**端到端学习（直接从像素到结果）**的可行性，颠覆了“手工特征优先”的传统观念，推动了后续更深网络（如 VGG、ResNet）的发展。

传统方法的局限​

  • LeNet 的不足：早期的卷积神经网络（如 LeNet）在小数据集上表现不错，但在更大、更真实的数据集（如图像分辨率更高、类别更多的场景）中效果有限。
  • 传统机器学习的套路：2012 年之前，计算机视觉主要依赖手工设计的特征（如 SIFT、HOG 等），流程是： 收集数据 → 手工预处理（如调整像素）→ 提取人工特征（如边缘、纹理）→ 用分类器（如支持向量机）识别。 当时研究者认为，数据和特征设计比算法更重要，机器学习算法（如神经网络）常被忽视。
  • 技术瓶颈：
    • 数据少：早期数据集规模小（如 UCI 数据集只有几百到几千张低分辨率图像）。
    • 硬件弱：CPU 计算能力不足，无法训练参数多的深层神经网络。
    • 缺少关键技巧：如合适的参数初始化方法、ReLU 激活函数、Dropout 正则化等。

架构​

比 LeNet 更深、更强大

  • 核心改进：

    • 层数更多：LeNet 只有几层，而 AlexNet 有 8 层（五个卷积层、两个全连接隐藏层和一个全连接输出层），能提取更复杂的特征（如底层边缘 → 高层物体部件 → 整体物体）。
    • 激活函数：用 ReLU 代替 Sigmoid，解决了 Sigmoid 在梯度反向传播时容易“梯度消失”的问题，训练更高效。
    • Dropout 正则化：在全连接层加入 Dropout，随机丢弃部分神经元，减少过拟合。
    • 数据增强：训练时对图像进行翻转、裁剪、变色等处理，增加数据多样性，提升模型鲁棒性。
    • 更大的卷积窗口与通道数：第一层用 11×11 的卷积核（LeNet 用 5×5），提取更大范围的特征；通道数更多（如 96、256 通道），捕捉更丰富的视觉信息。

  • 网络结构示例

    net = nn.Sequential(
        # 第一层：大卷积核+ReLU+最大池化
        nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
        nn.MaxPool2d(3, stride=2),
        # 后续卷积层：逐步缩小窗口，增加通道数
        nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
        nn.MaxPool2d(3, stride=2),
        # 全连接层：参数多，用Dropout防过拟合
        nn.Linear(6400, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10)  # 输出层（如Fashion-MNIST的10个类别）
    )

使用块的网络 VGG​

VGG 的核心思路：用“块”搭建网络​

  • 灵感来源：之前的 AlexNet 证明了深层网络的有效性，但没有统一的设计框架。VGG 提出用**重复的块（Block）**来构建网络，就像搭积木一样，每个块由多个卷积层和一个池化层组成。
  • 块的结构：
    • 每个 VGG 块包含 多个 3×3 的卷积层（通常 2-3 个），每个卷积层后接 ReLU 激活函数，并用 padding=1 保持图像尺寸不变。
    • 每个块的最后有一个 2×2 最大池化层，步幅为 2，将图像尺寸减半（例如从 224×224→112×112）。
    • 这样的设计让网络可以逐层提取更复杂的特征，同时通过池化层降低计算量。

VGG 网络的架构细节​

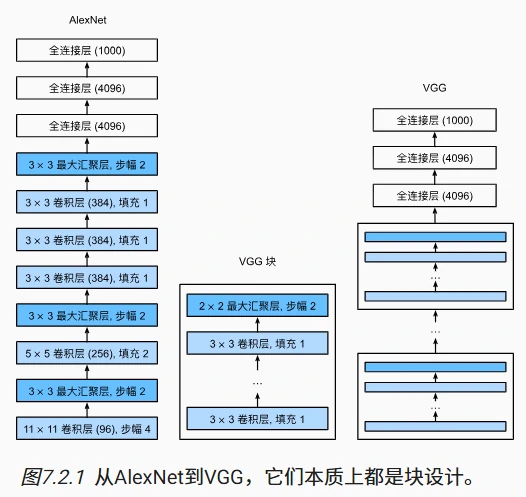VGG网络架构图 - 卷积层部分：

  • VGG 有多种变体（如 VGG-11、VGG-16、VGG-19），数字代表总层数。以 VGG-11 为例：

    • 由 5 个 VGG 块组成，每个块的卷积层数和输出通道数如下：
      • 块 1：1 个卷积层，64 通道
      • 块 2：1 个卷积层，128 通道
      • 块 3：2 个卷积层，256 通道
      • 块 4：2 个卷积层，512 通道
      • 块 5：2 个卷积层，512 通道
    • 每个块通过池化层将图像尺寸减半，最终尺寸从 224×224→7×7。

  • 全连接层部分：

    • 与 AlexNet 类似，包含 3 层全连接层（4096→4096→10），中间用 Dropout 防止过拟合，输出层对应分类类别（如 Fashion-MNIST 的 10 类）。

  • 代码实现：

    通过循环生成多个 VGG 块，例如：

    # 定义一个VGG块，包含num_convs个卷积层和1个池化层
    def vgg_block(num_convs, in_channels, out_channels):
        layers = []
        for _ in range(num_convs):
            layers.append(卷积层(3x3, 填充=1, 输出通道=out_channels))
            layers.append(ReLU激活函数)
            in_channels = out_channels
        layers.append(最大池化层(2x2, 步幅=2))
        return 组合这些层为一个块

网络中的网络 NiN​

NiN 的核心改进：用“小网络”替代全连接层​

  • 传统 CNN 的问题：像 AlexNet 和 VGG 这样的网络，在卷积层之后使用全连接层进行分类。全连接层会将空间特征（如图像的宽、高维度）压缩成一维向量，可能丢失空间结构信息，且容易过拟合（参数多）。
  • NiN 的解决方案：
    • 在每个像素的通道维度上应用一个“小型多层感知机（MLP）”，相当于用多个 1×1 卷积层模拟全连接层的计算，保留空间结构的同时增加非线性。
    • 最终用全局平均汇聚层替代全连接层，直接对每个通道的全局信息求和，输出分类结果，大幅减少参数数量。

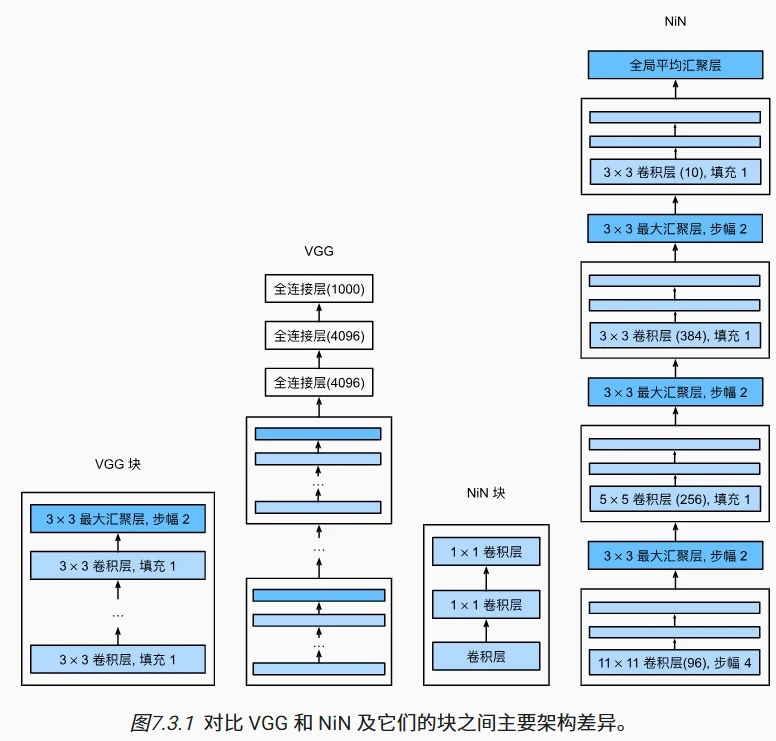
NiN 块的结构：三次卷积，增强特征表达​

  • 块的组成：每个 NiN 块包含 1 个普通卷积层 + 2 个 1×1 卷积层，结构如下：

    def nin_block(输入通道, 输出通道, 卷积核大小, 步幅, 填充):
        return 顺序连接：
            普通卷积层（提取空间特征）→ ReLU激活
            1×1卷积层（压缩通道或增加非线性）→ ReLU激活
            1×1卷积层（进一步处理特征）→ ReLU激活
    • 普通卷积层：负责提取传统的空间特征（如边缘、纹理）。
    • 1×1 卷积层：相当于在每个像素的通道维度上进行全连接运算，可理解为“每个像素自己的小神经网络”，能捕捉通道间的关联（例如，将 RGB 三通道的信息融合）。

  • 作用：通过多层卷积叠加，每个像素的特征会被更复杂地变换，增强模型对局部模式的表达能力。

NiN 网络架构：取消全连接，全局汇聚分类​

  • 整体结构：NiN 由多个 NiN 块和最大汇聚层交替组成，最后接全局平均汇聚层和输出层，具体如下：

    1. 卷积层部分：
      • 第一层：11×11 卷积（类似 AlexNet），提取大尺度特征，接最大池化（缩小尺寸）。
      • 中间层：5×5 和 3×3 卷积，逐步提取更细粒度特征，每次卷积后接最大池化。
      • 每个 NiN 块后通过池化层（如 3×3 最大池化，步幅 2）降低图像尺寸，减少计算量。
    2. 分类部分：
      • 最后一个 NiN 块输出通道数等于类别数（如 Fashion-MNIST 的 10 类）。
      • 用全局平均汇聚层替代全连接层：对每个通道的所有像素求平均值，得到长度为通道数的一维向量，直接作为分类器输入。
      • 优点：避免全连接层的过拟合问题，参数数量大幅减少（例如，假设最后一层是 10 通道的 7×7 特征图，全局平均汇聚直接求和，无需权重参数）。

NiN 与 AlexNet/VGG 的对比​

维度AlexNet/VGGNiN
全连接层有，参数多，易过拟合无，用全局平均汇聚替代
特征处理卷积层提取空间特征，全连接层压缩特征每个像素用 1×1 卷积（小网络）处理特征，保留空间结构
参数数量多（全连接层占大部分参数）少（取消全连接层，1×1 卷积参数少）
计算效率计算量大，需更多显存计算量较小，但训练时间可能因多层卷积增加

含并行连结的网络 GoogleNet​

GoogLeNet 的核心创新：Inception 块​

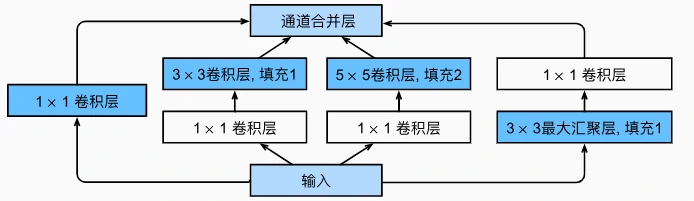
Inception 块的设计思想​
  • 并行多分支结构：每个 Inception 块包含 4 条并行路径，分别使用不同大小的卷积核（1×1、3×3、5×5）和最大池化层，从多个尺度提取特征。
    • 路径 1：1×1 卷积层，捕捉全局特征或压缩通道数。
    • 路径 2：1×1 卷积层（降维）+ 3×3 卷积层，捕捉中等尺度特征。
    • 路径 3：1×1 卷积层（降维）+ 5×5 卷积层，捕捉大尺度特征。
    • 路径 4：3×3 最大池化层 + 1×1 卷积层，捕捉边缘等底层特征并调整通道数。
  • 特征融合：将 4 条路径的输出在通道维度上拼接，形成包含多尺度信息的特征图。
设计优势​
  • 多尺度特征捕捉：不同大小的卷积核可提取不同范围的特征（如 1×1 捕捉细节，5×5 捕捉整体结构），提升模型对复杂图像的适应性。
  • 计算效率优化：通过 1×1 卷积层降维（如路径 2、3），减少参数量和计算量。例如，先将输入通道数从$( C )$降至$( c )$，再进行 3×3 卷积，计算量从$( C \times 3 \times 3 \times H \times W )$降至$( c \times 3 \times 3 \times H \times W )$（$( c \ll C )$）。
  • 避免单一卷积核的局限性：传统网络使用固定大小的卷积核，可能遗漏其他尺度的特征，而 Inception 块通过并行结构实现“特征互补”。

GoogLeNet 整体架构​

层级结构​

GoogLeNet 由输入层、多个 Inception 块、池化层和全局平均汇聚层组成，共包含 9 个 Inception 块，整体结构分为 5 个模块（b1 到 b5）：

  • 模块 b1： 7×7 卷积层（64 通道，步幅 2），用于提取基础特征，后接 3×3 最大池化层（步幅 2）降低分辨率。

  • 模块 b2： 1×1 卷积层（64 通道）降维，接 3×3 卷积层（192 通道），后接 3×3 最大池化层（步幅 2）。

  • 模块 b3：

    • 串联 2 个 Inception 块：
      • 第一个 Inception 块：输出通道数为 64（1×1）+ 128（3×3）+ 32（5×5）+ 32（池化）= 256。
      • 第二个 Inception 块：输出通道数为 128 + 192 + 96 + 64 = 480。
    • 后接 3×3 最大池化层（步幅 2）。

  • 模块 b4：

    • 串联 5 个 Inception 块，逐步增加通道数（如从 512 到 832），捕捉更复杂的多尺度特征。
    • 后接 3×3 最大池化层（步幅 2）。

  • 模块 b5： 串联 2 个 Inception 块，最终通过全局平均汇聚层将特征图压缩为一维向量，接全连接层输出分类结果（如 1000 类）。

  • 取消全连接层：与 NiN 类似，GoogLeNet 在最后使用全局平均汇聚层替代全连接层，减少参数数量并避免过拟合。

  • 深度与宽度的平衡：通过堆叠多个 Inception 块增加网络深度，同时通过并行分支扩展特征的宽度（通道数），在保持计算效率的前提下提升模型能力。

Inception 块的代码示例​

class Inception(nn.Module):
    def __init__(self, in_channels, c1, c2, c3, c4):
        super().__init__()
        # 四条路径的定义
        self.p1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        self.p2 = nn.Sequential(
            nn.Conv2d(in_channels, c2[0], kernel_size=1),
            nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        )
        self.p3 = nn.Sequential(
            nn.Conv2d(in_channels, c3[0], kernel_size=1),
            nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        )
        self.p4 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            nn.Conv2d(in_channels, c4, kernel_size=1)
        )

    def forward(self, x):
        p1 = F.relu(self.p1(x))
        p2 = F.relu(self.p2(x))
        p3 = F.relu(self.p3(x))
        p4 = F.relu(self.p4(x))
        return torch.cat((p1, p2, p3, p4), dim=1)  # 通道维度拼接

批量规范化​

为什么需要批量规范化​

训练深层神经网络时会遇到以下问题：

  1. 内部协变量偏移（Internal Covariate Shift）： 随着训练进行，中间层的输出分布会发生变化（例如，某层输出的均值和方差逐渐变大或变小），导致模型需要不断调整参数来适应这种变化，训练速度变慢，甚至出现梯度消失/爆炸。
  2. 参数尺度不一致： 不同层的输出可能具有不同的尺度（如一层输出是 0-1，另一层是 100-200），导致优化器难以高效更新参数。
  3. 过拟合风险： 深层网络容易过拟合，需要更强的正则化手段。

批量规范化的核心思路：在每层的输入前对数据进行标准化（均值为 0，方差为 1），并引入可学习的缩放和偏移参数，让网络自动调整最优分布，从而加速训练并提升泛化能力。

批量规范化的工作原理​

1. 训练阶段​

对于一个小批量数据$( B )$，批量规范化的计算步骤如下：

  • 标准化： $\hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$ 其中，$( \mu_B )$是小批量的均值，$( \sigma_B^2 )$是方差，$( \epsilon )$是一个很小的常数（避免除以零）。
  • 缩放与偏移： $[ y = \gamma \odot \hat{x} + \beta ]$ $( \gamma )$（缩放参数）和$( \beta )$（偏移参数）是可学习的参数，用于调整标准化后的数据分布（例如，恢复有用的特征尺度）。
2. 预测阶段​
  • 由于预测时通常处理单样本或小批量数据，无法计算可靠的均值和方差，因此使用训练阶段记录的**移动平均值（moving average）**来替代$( \mu_B )$和$( \sigma_B^2 )$，确保输出的稳定性。

批量规范化在不同层中的应用​

1. 全连接层​
  • 应用位置：全连接层的仿射变换（$( Wx + b )$）之后，激活函数之前。
  • 标准化对象：在特征维度上进行（即对每个特征的所有样本求均值和方差）。
2. 卷积层​
  • 应用位置：卷积层之后，激活函数之前。
  • 标准化对象：在通道维度上进行。对于每个通道，收集该通道在所有空间位置和样本上的值，计算均值和方差（例如，输入形状为$( (批量大小, 通道数, 高, 宽) )$，则在批量、高、宽维度上求均值/方差，保留通道维度）。

批量规范化的关键作用​

  1. 加速训练收敛： 通过固定中间层的分布，减少内部协变量偏移，使梯度更新更稳定，允许使用更大的学习率，从而加快收敛速度。
  2. 缓解梯度消失/爆炸： 标准化后的数据分布更接近激活函数的有效区间（如 ReLU 的非负区间），避免神经元进入饱和区域，保持梯度有效性。
  3. 充当正则化角色： 训练时使用小批量的均值/方差引入了一定的噪声，类似数据增强，有助于抑制过拟合（尤其在批量较小时，噪声效应更明显）。
  4. 允许更灵活的网络设计： 例如，使用批量规范化后，网络对权重初始化的敏感度降低，更容易训练深层网络（如 100 层以上的 ResNet）。

代码实现与注意事项​

import torch
import torch.nn as nn

class BatchNorm(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.9):
        super().__init__()
        self.eps = eps
        self.momentum = momentum
        # 可学习的缩放和偏移参数
        self.gamma = nn.Parameter(torch.ones(num_features))
        self.beta = nn.Parameter(torch.zeros(num_features))
        # 移动平均的均值和方差（预测时使用）
        self.register_buffer('moving_mean', torch.zeros(num_features))
        self.register_buffer('moving_var', torch.ones(num_features))

    def forward(self, x):
        if self.training:
            # 训练阶段：计算当前小批量的均值和方差
            if x.dim() == 2:  # 全连接层输入（批量, 特征）
                mean = x.mean(dim=0)
                var = x.var(dim=0, unbiased=False)
            else:  # 卷积层输入（批量, 通道, 高, 宽）
                mean = x.mean(dim=(0, 2, 3), keepdim=True)
                var = x.var(dim=(0, 2, 3), keepdim=False)
            # 更新移动平均
            self.moving_mean = self.moving_mean * self.momentum + mean * (1 - self.momentum)
            self.moving_var = self.moving_var * self.momentum + var * (1 - self.momentum)
        else:
            # 预测阶段：使用移动平均的均值和方差
            mean = self.moving_mean
            var = self.moving_var
        # 标准化 + 缩放偏移
        x_hat = (x - mean) / torch.sqrt(var + self.eps)
        return self.gamma * x_hat + self.beta
  • 批量大小的影响：批量越大，均值和方差的估计越准确，训练效果越好；批量为 1 时无法计算（均值相减后全为 0）。
  • 位置选择：通常位于卷积层或全连接层之后，激活函数之前，但某些架构（如 ResNet）可能有不同安排。
  • 与 Dropout 的配合：两者可共存，但需注意顺序（通常先 BN，再 Dropout 或激活函数）。

ResNet残差网络​

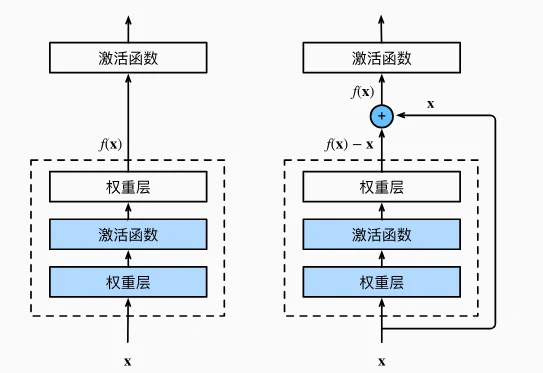
传统神经网络层数加深时，性能可能下降，效果可能变差（梯度消失或爆炸问题）。而Residual Network通过残差连接能解决该问题。 核心设计：传统网络层直接拟合目标映射$(f(x))$，而残差块拟合的是“残差映射”$(f(x)-x)$。

  • 如果理想输出接近输入（恒等映射），只需让残差部分接近 0，学习难度大幅降低。（不接近就没大用）
  • 残差块通过“跨层连接”（捷径）将输入直接加到输出上，避免信息在深层传播中丢失。（这个很重要）

残差块​

一个典型的残差块由以下部分组成： 卷积层：通常包含 2-3 个卷积操作（如 3×3 卷积），用于提取特征； 批归一化（Batch Normalization）：加速训练，缓解梯度消失； 激活函数：如 ReLU，引入非线性； 跳跃连接（Skip Connection）：将输入 x 直接加到卷积层的输出上（需保证维度匹配）。 若输入与输出通道数或尺寸不同，用 1×1 卷积调整输入（use_1x1conv=True），确保能与输出相加。 残差网络

ResNet整体架构​

  • 基础模块： 由多个残差块组成，每个模块内的残差块输出通道数相同，且第一个残差块可能通过步幅和 1×1 卷积调整尺寸和通道数。
    • 例如：ResNet-18 包含 4 个模块，每个模块有 2 个残差块，共 18 层（含卷积和全连接层）。
  • 网络流程：
    1. 初始层：7×7 卷积（步幅 2）+ 批量归一化 + ReLU + 3×3 最大池化（步幅 2），缩小尺寸并提取特征。
    2. 残差模块：依次将通道数从 64 翻倍到 128、256、512，同时尺寸减半（如从 56×56 到 28×28，再到 14×14、7×7）。
    3. 结尾层：全局平均池化 + 全连接层，输出分类结果（如图 7.6.4）。

DenseNet稠密连接网络​

从 ResNet 到 DenseNet​

  • ResNet 的局限与灵感： ResNet 通过“跨层相加”让网络学习“残差”（$(f(x) = x + g(x))$），解决了深层网络训练难题。但 DenseNet 进一步思考：如果把每一层的输出连接（而非相加）起来，是否能像泰勒展开一样，让网络学习更丰富的特征组合？
    • 核心区别：ResNet 的跨层连接是“相加”（保持通道数不变），而 DenseNet 是“连结”（通道数累加），如图 7.7.1 所示。
  • 稠密连接的数学直观： 假设输入为$(x)$，第一层输出为$(f_1(x))$，第二层输入是$(x)$和$(f_1(x))$的连结，输出为$(f_2([x, f_1(x)]))$，依此类推。最终将所有层的特征连结，形成更全面的特征表示（如图 7.7.2）。

稠密块（Dense Block）​

  • 结构设计： 每个稠密块包含多个“卷积块”，每个卷积块的结构为：批量归一化（BN）→ ReLU 激活 → 3×3 卷积。
    • 前向传播时，每一层的输入是前面所有层输出的连结，输出则与输入连结后传递给下一层。
    • 例如：输入通道数为 3，增长率（每层输出通道数）为 10，经过 2 层稠密块后，输出通道数为$(3 + 2×10 = 23)$（如图 7.7.3 示例）。
  • 增长率的意义： 增长率控制每层新增的通道数，是 DenseNet 的核心超参数。较小的增长率即可通过多层连结积累丰富特征，避免了传统网络因层数深而导致的特征“稀释”问题。

过渡层（Transition Layer）：控制复杂度的“阀门​

  • 为什么需要过渡层？ 稠密块会不断累加通道数，导致计算量爆炸。过渡层的作用是：
    1. 降维：用 1×1 卷积减少通道数（如减半）。
    2. 降采样：用平均池化（步幅 2）缩小高和宽，降低计算复杂度。
  • 结构示例： 过渡层包含 BN→ReLU→1×1 卷积 → 平均池化。例如，输入通道数 23，过渡层输出通道数设为 10，则高和宽减半，通道数变为 10（如图 7.7.4 示例）。

DenseNet 整体架构：特征重用​

  • 网络流程：
    1. 初始层：与 ResNet 类似，7×7 卷积（步幅 2）+ BN + ReLU + 3×3 最大池化（步幅 2），缩小尺寸并提取初始特征。
    2. 稠密块+过渡层交替：
      • 通常使用 4 个稠密块，每个块内有若干卷积层（如 4 层），增长率设为 32。
      • 每个稠密块后接过渡层，通道数减半，尺寸减半（如从 56×56 到 28×28）。
    3. 结尾层：全局平均池化 + 全连接层，输出分类结果。
  • 与 ResNet 的对比：
    • ResNet 通过“残差块”实现跨层相加，保持通道数不变；DenseNet 通过“稠密块”实现跨层连结，通道数逐层增加。
    • DenseNet 的特征重用更充分，但显存消耗更高（因连结操作存储中间结果）。